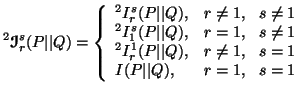 |
(4.10) |
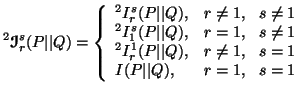 |
(4.10) |
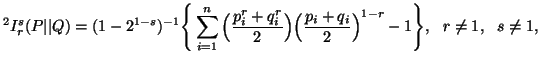
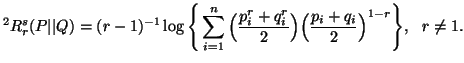
The second generalizations of unified![]() divergence
measure is given by
divergence
measure is given by
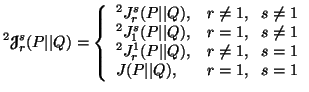 |
(4.11) |
![$\displaystyle ^2J^s_r(P\vert\vert Q)=2(1-2^{1-s})^{-1}\Bigg\{\Big[\sum_{i=1}^......-r}_iq^r_i\over2}\Big)\Big]^{s-1\over r-1} }-1\Bigg\},\ \ r\neq 1,\ \ s\neq 1$](img1077.gif)
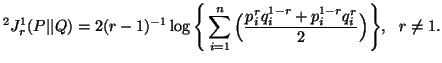
Note 4.6. Measures appearing in the unified expressions (4.6)
and (4.7) are due to Taneja (1989) [105].
Most of the measures appearing in the unified expressions (4.10) and (4.11)
are due to Taneja (1984b;1987;1989) [102],
[103], [105]
except the measures![]() and
and ![]() .
The measure
.
The measure ![]() is due to Burbea (1984) [17] and the measure
is due to Burbea (1984) [17] and the measure ![]() is due to Rathie and Sheng (1981) [80] and
Burbea and Rao (1982a;b) [18], [19].
is due to Rathie and Sheng (1981) [80] and
Burbea and Rao (1982a;b) [18], [19].