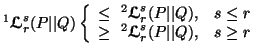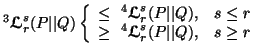![]() and
and![]()
Similar to expression (4.3) we can write
![]() and
and![]()
where ![]() is as given in (4.19).
is as given in (4.19).
Property 4.24. (Nonnegativity)![]() and
and![]() with equality iff
with equality iff ![]() .
.
Property 4.25. (Continuity)![]() and
and![]() are continuous functions of the pair
are continuous functions of the pair ![]() and are also continuous with respect to the parameters
and are also continuous with respect to the parameters ![]() and
and ![]() .
.
Property 4.26. (Symmetry)![]() and
and![]() are symmetric functions of their arguments in pair, i.e.,
are symmetric functions of their arguments in pair, i.e.,
![]()
![]() and 4), where
and 4), where ![]() is any permutation from
is any permutation from ![]() to
to ![]() .
.
Property 4.27. (Nonnaditivity). We have
![]()
for all ![]() ,
, ![]() and
and ![]() ,
, ![]() and
and ![]() .
.
Property 4.28. (Monotonicity).![]() (
(![]() and
and ![]() )
are increasing functions of
)
are increasing functions of ![]() (
(![]() fixed) and of
fixed) and of ![]() (
(![]() fixed). In particular, when
fixed). In particular, when ![]() ,
the result still holds.
,
the result still holds.
Property 4.29. (Convexity).![]() (
(![]() and
and ![]() )
are convex functions of the pair of probability distributions
)
are convex functions of the pair of probability distributions ![]() for
for ![]() .
.
Property 4.30. (Schur-convexity).![]() (
(![]() and
and ![]() )
are Schur-convex functions in the pair
)
are Schur-convex functions in the pair ![]() .
.
Property 4.31. (Generalized data processing inequalities). We have
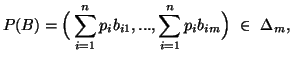
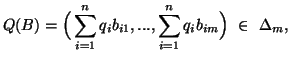
Property 4.32. (Strong generalized data processing inequalities).
If the stochastic matrix B given in the property 4.31 is such that there
exists an ![]() for which
for which![]() ,
, ![]() ,
then we have
,
then we have
![]() and
and![]()
Property 4.33. (Inequalities among the measures). We have
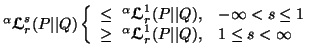 for
for 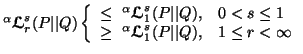 for
for