We observe the measures
We observe the measures ![]() (
(![]() and
and ![]() )
) ![]() (
(![]() and
and ![]() )
and
)
and![]() (
(![]() and
and ![]() )
are continuous with respect to the parameters
)
are continuous with respect to the parameters ![]() and
and ![]() .
This allows us to write them in the following simplified forms:
.
This allows us to write them in the following simplified forms:
![]()
Also we can write
![]()
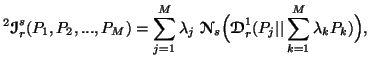
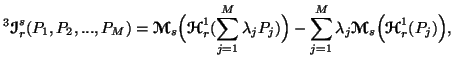
![]() and
and![]()
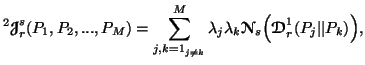
![]() and
and![]()
and
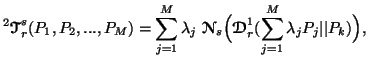
where ![]() and
and ![]() are as given by (3.10) and (4.4) respectively.
are as given by (3.10) and (4.4) respectively.