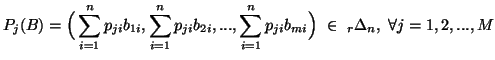In this subsection we shall give some properties of
In this subsection we shall give some properties of ![]() dimensional
unified
dimensional
unified ![]() measures
measures![]() ,
, ![]() and
and![]() (
(![]() and 3).
and 3).
Property 5.1. The measures ![]() (
(![]() and 2),
and 2), ![]() (
(![]() and 3) and
and 3) and ![]() (
(![]() and 3) are nonnegative for all
and 3) are nonnegative for all ![]() and any
and any ![]() are zero iff
are zero iff![]() .
The nonnegativity of
.
The nonnegativity of ![]() follows under the conditions when either
follows under the conditions when either![]() or
or ![]() with
with ![]() .
.
Property 5.2. For all ![]() ,
we have
,
we have
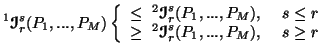
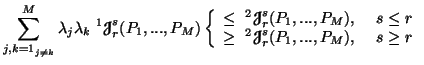
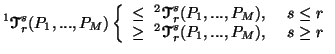
Property 5.3. For all ![]() ,
we have
,
we have
Property 5.4. For all ![]() ,
, ![]() and 2, we have
and 2, we have
![]()
Property 5.5. The measures ![]() (
(![]() =1
and 2),
=1
and 2), ![]() (
(![]() =1,2
and 3) and
=1,2
and 3) and ![]() (
(![]() =1,2
and 3) are increasing functions of
=1,2
and 3) are increasing functions of ![]() (
(![]() fixed) and of
fixed) and of ![]() (
(![]() fixed). In particular, when
fixed). In particular, when ![]() ,
the result still holds.
,
the result still holds.
Property 5.6. For ![]()
![]() (0,
(0,![]() ),
), ![]()
![]() (
(![]() ),
), ![]() =1
and 2, the measures
=1
and 2, the measures![]() ,
, ![]()
![]() and
and ![]() are Schur-convex functions of
are Schur-convex functions of ![]() i.e.,
i.e., ![]() implies
implies
Property 5.7. (Generalized data processing inequalities).
For ![]()
![]() (0,
(0,![]() ),
), ![]()
![]() (
(![]() ),
), ![]() =1
and 2, we have
=1
and 2, we have
![]()