Next:Mutual
InformationUp:Shannon's
Entropy
Previous:Properties
of Shannon's Entropy Go to:Table
of Contents
Multivariate Entropies
Let 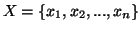 and
and 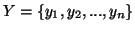 be two discrete finite random variables with joint and individual probability
distributions given by
be two discrete finite random variables with joint and individual probability
distributions given by
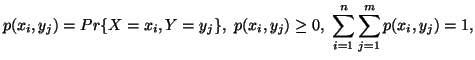
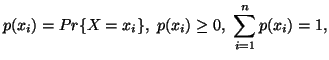 and
and
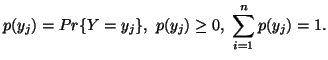 The conditional probability of
The conditional probability of 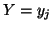 given
given 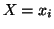 is given by
is given by
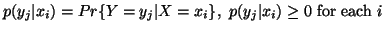 with
with
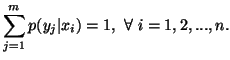 The conditional probability of
The conditional probability of 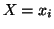 given
given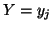 is given by
is given by
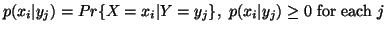 with
with
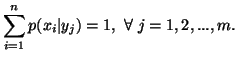 The following relations are well known in the literature:
The following relations are well known in the literature:
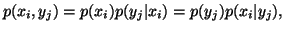
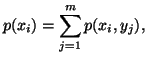 and
and
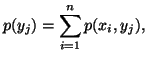 for each
for each 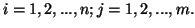 When
When 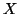 and
and 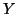 are independent, we have
are independent, we have
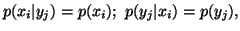
and
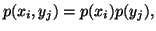 for each
for each 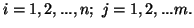 Based on the above notations, we give now the joint, individual
and conditional measures of uncertainty. The joint measure
of uncertainty of
Based on the above notations, we give now the joint, individual
and conditional measures of uncertainty. The joint measure
of uncertainty of 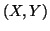 is given by
is given by
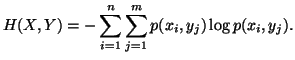 The individual measures of uncertainty of
The individual measures of uncertainty of 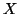 and
and 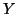 are given by
are given by
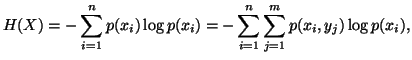
and
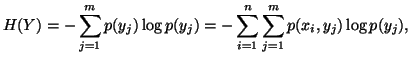 respectively The conditional uncertainty of Y given
respectively The conditional uncertainty of Y given 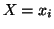 is given by
is given by
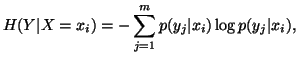 for each
for each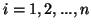 .
The conditional uncertainty of
.
The conditional uncertainty of 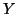 given
given 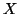 is the average uncertainty of
is the average uncertainty of 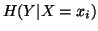 with the probabilities
with the probabilities 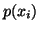 is given by
is given by
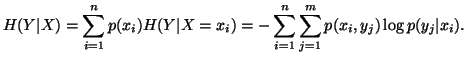 Similarly, we can write the conditional uncertainty of
Similarly, we can write the conditional uncertainty of 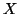 given
given 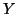 as
as
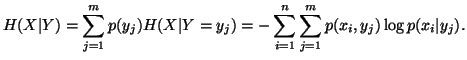 In case of three random variables
In case of three random variables 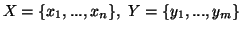 and
and 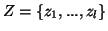 with their respective probability distributions, we have the following
measures of uncertainty
with their respective probability distributions, we have the following
measures of uncertainty
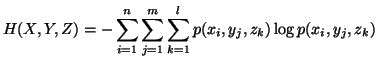
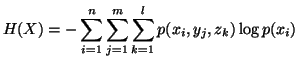
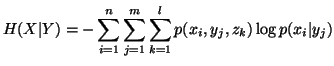
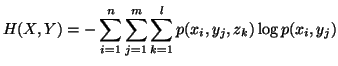
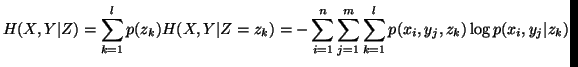
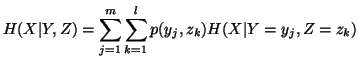
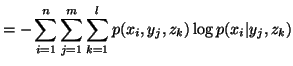 etc..
etc..
The following properties hold for the above uncertainty measures.
Property 1.38. We have
-
(i)
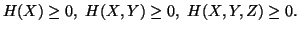
-
(ii)
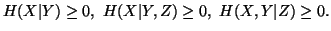
Property 1.39. We have
-
(i)
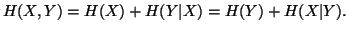
-
(ii)
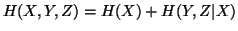
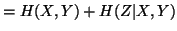
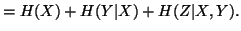
Property 1.40. We have
-
(i)
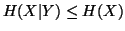 ,
with equality iff
,
with equality iff 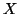 and
and 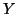 are independent i.e.,
are independent i.e., 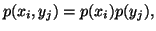
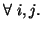
-
(ii)
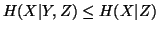 ,
with equality iff
,
with equality iff 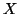 and
and 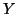 are conditionally independent given
are conditionally independent given 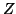 i.e.,
i.e., 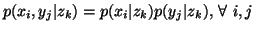 and each
and each 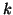 .
.
-
(iii)
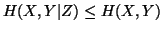 ,
with equality iff
,
with equality iff 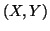 and
and 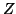 are independent i.e.,
are independent i.e., 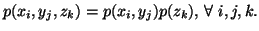
Note 1.2. Since the random variables 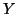 and
and 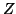 are symmetric among them, then from the property 1.40(ii), we can write
are symmetric among them, then from the property 1.40(ii), we can write
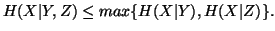
Property 1.41. We have
-
(i)
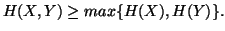
-
(ii)
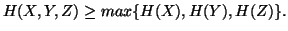
-
(iii)
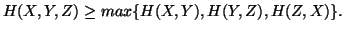
-
(iv)
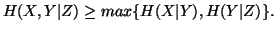
Property 1.42. We have
-
(i)
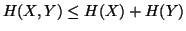 ,
with equality iff
,
with equality iff 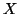 and
and 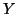 are independent i.e.,
are independent i.e., 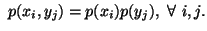
-
(ii)
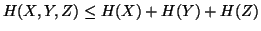 ,
with equality iff
,
with equality iff 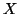 ,
, 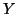 and
and 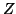 are independent i.e., iff
are independent i.e., iff 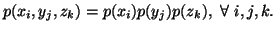
-
(iii)
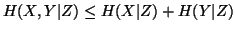 ,
with equality iff
,
with equality iff 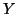 and
and 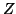 are conditionally independent given
are conditionally independent given 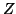 i.e., iff
i.e., iff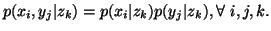
Property 1.43. We have
-
(i)
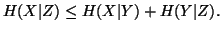
-
(ii) If
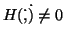 ,
then
,
then
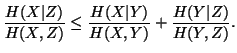
Property 1.44. For each k, define
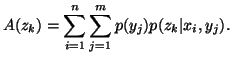 Then
Then
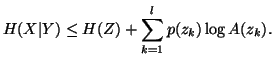 Property 1.45. Let
Property 1.45. Let 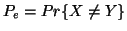 .
Then
.
Then
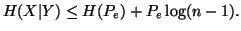
Note 1.3. The property 1.45 is famous as "Fano-inequality".
For four discrete random variables 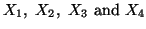 the following property holds.
the following property holds.
Property 1.46. We have
-
(i)
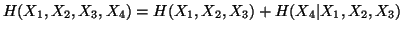
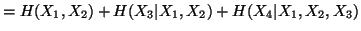
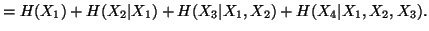
-
(ii)
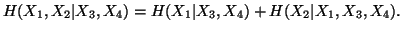
-
(iii)
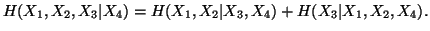
-
(iv)
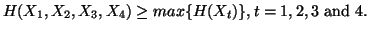
-
(v)
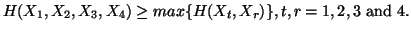
-
(vi)
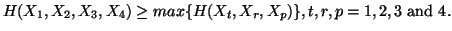
-
(vii)
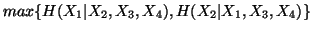
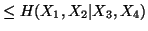
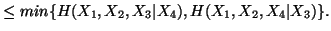
-
(viii)
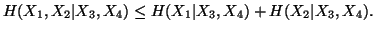
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
![]() and
and ![]() be two discrete finite random variables with joint and individual probability
distributions given by
be two discrete finite random variables with joint and individual probability
distributions given by
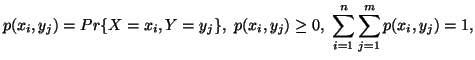
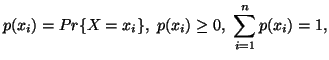
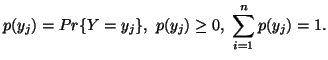
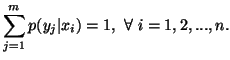
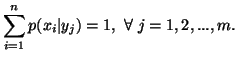
![]()
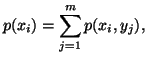
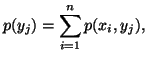
![]()
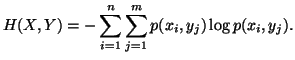
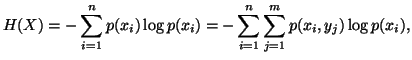
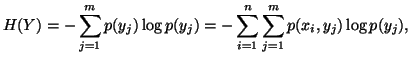
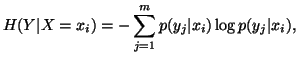
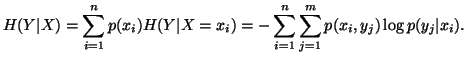
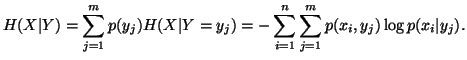
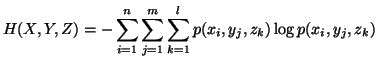
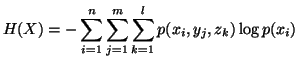
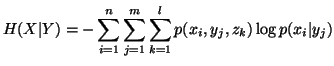
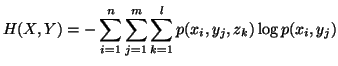
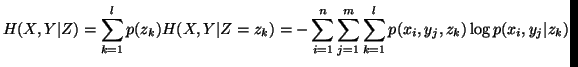
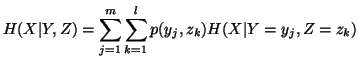
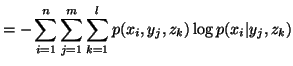
![]()
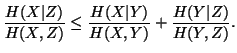
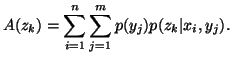
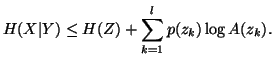
![]()
![]() the following property holds.
the following property holds.