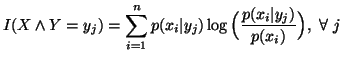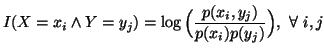Next:Information
Measures for DiscreteUp:Shannon's
Entropy
Previous:Multivariate
Entropies Go to:Table
of Contents
Mutual Information
Let us consider the following differences
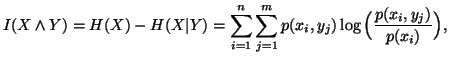
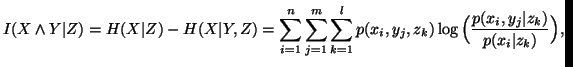 and
and
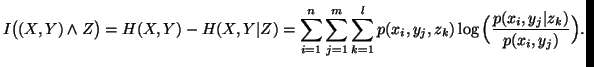
In view of the property 1.40, the following property holds.
Property 1.47. We have
-
(i)
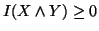 with equality iff
with equality iff 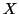 and
and 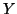 are independent.
are independent.
-
(ii)
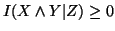 with equality iff
with equality iff 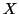 and
and 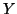 are conditionally independent given
are conditionally independent given 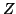 .
.
-
(iii)
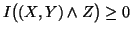 with equality iff
with equality iff 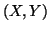 and
and 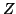 are independent.
are independent.
The above measures are famous in the literature as
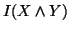 : mutual information among the random variables
: mutual information among the random variables 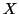 and
and 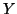 ;
;
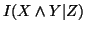 : mutual information among the random variables
: mutual information among the random variables 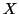 and
and 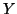 given
given 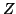 ;
;
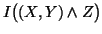 : mutual information among the random variables
: mutual information among the random variables 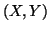 and
and 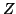 .
.
We can write
![$\displaystyle I(X\wedge Y)=E_Y \big[I(X\wedge Y=y_j)\big] = E_{XY} \big[ I(X=x_i \wedge Y=y_j) \big],$](img260.gif) where
where
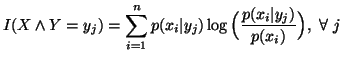 and
and
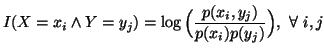 In view of the above representation,
In view of the above representation, 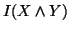 sometimes understood as the average or the conditional mutual
information of
sometimes understood as the average or the conditional mutual
information of 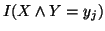 or of
or of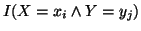 .
The expression
.
The expression 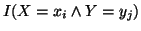 is known as per-letter information, and it may be negative. It is
nonnegative iff
is known as per-letter information, and it may be negative. It is
nonnegative iff 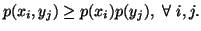 Similarly, we can write expressions for
Similarly, we can write expressions for 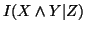 and
and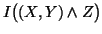 .
In fact, the following properties hold.
.
In fact, the following properties hold.
Property 1.48. We have
-
(i)
![$ E_X \big[ I(X=x_i\wedge Y)\big] = E_Y\big[ I(X\wedge Y=y_j)\big] .$](img266.gif)
-
(ii)
![$ E_{YZ} \big[ I(X\wedge Y=y_j\vert Z=z_k)\big] = E_{XZ}\big[I(X=x_i\wedge Y\vert Z=z_k)\big] .$](img267.gif)
-
(iii)
![$ E_Z \big[ I\big((X,Y)\wedge Z=z_k\big)\big] = E_{XY}\big[ I\big((X=x_i,Y=y_j)\wedge Z\big) \big] .$](img268.gif)
Property 1.49. We have
-
(i)
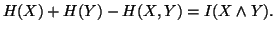
-
(ii)
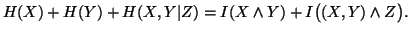
-
(iii)
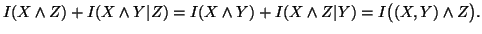
Property 1.50. We have
-
(i)
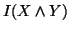 is a convex
is a convex  function of the probability distribution
function of the probability distribution 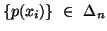 .
.
-
(ii)
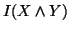 is a convex
is a convex  function of the probability distribution
function of the probability distribution 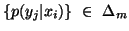 .
.
Property 1.51. We have
-
(i)
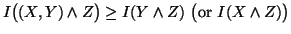 ,
with equality iff
,
with equality iff 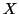 (or resp.
(or resp. 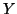 )
and
)
and 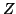 are conditionally independent given Y.
are conditionally independent given Y.
-
(ii)
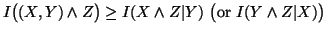 ,
with equality iff
,
with equality iff 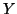 (or resp.
(or resp. 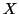 )
and
)
and 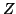 are independent.
are independent.
Property 1.52. If 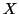 and
and 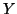 are conditionally independent given
are conditionally independent given 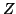 ,
then
,
then
-
(i)
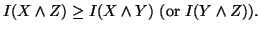
-
(ii)
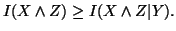
Property 1.53. We have
-
(i)
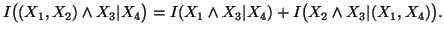
-
(ii)
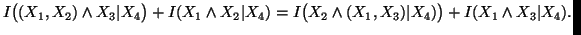
-
(iii)
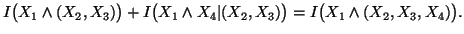
-
(iv)
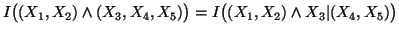
21-06-2001
Inder Jeet Taneja
Departamento de Matemática - UFSC
88.040-900 Florianópolis, SC - Brazil
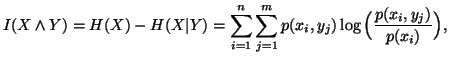
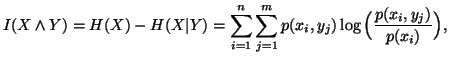
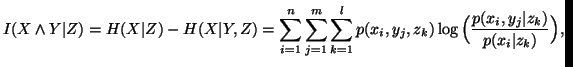
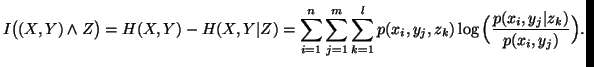
![]() : mutual information among the random variables
: mutual information among the random variables ![]() and
and ![]() ;
;
![]() : mutual information among the random variables
: mutual information among the random variables ![]() and
and ![]() given
given ![]() ;
;
![]() : mutual information among the random variables
: mutual information among the random variables ![]() and
and ![]() .
.