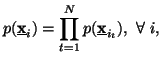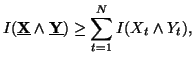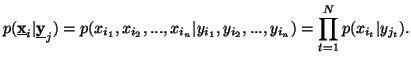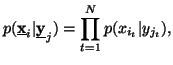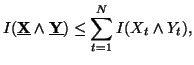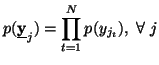Let us consider a random vector
Let us consider a random vector ![]() ,
where
,
where ![]() 's
are the discrete finite random variables. The distribution of
's
are the discrete finite random variables. The distribution of ![]() i.e., joint distribution of
i.e., joint distribution of ![]() is the function of
is the function of![]() ,
where each
,
where each ![]() is the range of
is the range of ![]() .
The entropy of a discrete random vector
.
The entropy of a discrete random vector ![]() is defined as
is defined as
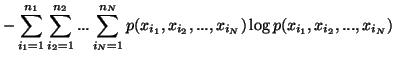 |
|||
where
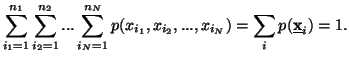
Similarly, we can write other measures given in section 1.4 for the discrete random vectors. Obviously, the properties 1.38 to 1.53 hold for discrete random vectors. We also have the following extra properties.
Property 1.54. We have
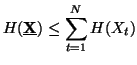
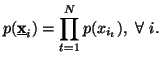
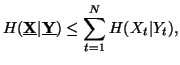
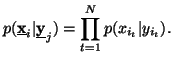
![]()
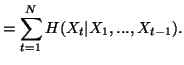
Note 1.4. The above property is famous as"Chain Rule".
Property 1.57. We have the following sequence of inequalities
![]()
Property 1.58. We have
Property 1.60. If the components![]() of X are independent i.e.,
of X are independent i.e.,