2. Inverse semigroupoids

2.1. Exel and graphed semigroupoids

We will now define semigroupoids, which are generalizations of both semigroups and categories. Every category $\mathcal{C}$ comes with an underlying graph structure, where vertices and arrows correspond respectively to objects and morphisms of $\mathcal{C}$. However, the vertex set of $\mathcal{C}$ can always be recovered from the arrow set, by identifying each object to its corresponding identity morphism, and so categories may be defined purely in terms of their arrow space. This becomes an issue in the case of semigroupoids, where we do not have identity elements (or something similar) anymore. We have two working definitions of semigroupoids: One purely algebraic, introduced by Exel in [MR2754831], and one where we assume an underlying graph structure, introduced by Tilson in [MR915990]. It should be noted that every semigroupoid in the sense of Tilson is a semigroupoid in the sense of Exel (Proposition 2.11).

To avoid any confusion, we will use capital greek letters $\Lambda,\Gamma,\ldots$ to denote semigroupoids in the sense of Exel, without a priori underlying graph structures. These are called simply semigroupoids, or Exel semigroupoids whenever such precision is warranted. Capital caligraphic latin letters $\mathcal{S},\mathcal{T},\ldots$ will be used to denote semigroupoids in the sense of Tilson, with an underlying graph structure, and these will always be called graphed semigroupoids.

Definition 2.1 ([MR2754831]).

An Exel semigroupoid or simply semigroupoid is a set $\Lambda$ equipped with a subset $\Lambda^{[2]}\subseteq\Lambda\times\Lambda$ and a product map $\mu\colon\Lambda^{[2]}\to\Lambda$, denoted by concatenation, $\mu(f,g)=fg$, which is associative in the following sense: For all $f,g,h\in\Lambda$, the statements

  1. $(f,g)\in\Lambda^{[2]}$ and $(g,h)\in\Lambda^{[2]}$;

  2. $(f,g)\in\Lambda^{[2]}$ and $(fg,h)\in\Lambda^{[2]}$;

  3. $(g,h)\in\Lambda^{[2]}$ and $(f,gh)\in\Lambda^{[2]}$;

are equivalent and in case any (all) of them holds, we have $(fg)h=f(gh)$. If necessary for precision, we will say instead that the triple $(\Lambda,\Lambda^{[2]},\mu)$ is a semigroupoid.

We use square brackets when denoting the subset $\Lambda^{[2]}$ of $\Lambda\times\Lambda$ to stress the fact that $\Lambda$ has no graph structure. Moreover, instead of saying that a pair $(f,g)$ belongs to $\Lambda^{[2]}$ we may simply state that “the product $fg$ is (well-)defined”.

The product of subsets of a semigroupoid $\Lambda$ is regarded in the standard manner: If $A,B\subseteq\Lambda$, the set $AB$ consists of all products $ab$ which are defined, where $a\in A$ and $b\in B$ - that is, $AB=\mu((A\times B)\cap\Lambda^{[2]})$. If $a\in\Lambda$, the products $aA$ and $Aa$ are defined similarly.

The associativity condition on the product may be regarded as follows: if any of the products $(fg)h$ or $f(gh)$ are defined, then the other product is also defined and they are equal, so we simply denote it $fgh$. Also, if $fg$ and $gh$ are both defined, $fgh$ is also defined. This allows us to move parentheses at will during computations.

Example 2.2.

Let $\theta$ be a left action of a group $G$ on a set $X$. Consider the disjoint union $\Lambda\defeq G\sqcup X$. We make $\Lambda$ into a semigroupoid by extending the product of $G$ to a partial product on $\Lambda$ with the action, viz. $gx=\theta_g(x)$ for all $g\in G$ and $x\in X$.

This is an alternative to the more useful construction of a transformation groupoid, which is a particular case of a semidirect product of semigroupoids (see Subection 2.4).

Let us look at some counter-examples for the associativity condition, where some of items (i)-(iii) are valid but the others are not.

Example 2.3.

Let $\Lambda=\left\{f,g,h\right\}$, and define $fg=f$ and $gh=h$. Then $fg$ and $gh$ are defined, but neither $(fg)h$ nor $f(gh)$ are defined.

Example 2.4.

Let $\Lambda=\left\{f,g,h\right\}$, and define $fg=g$, $gh=h$. Then $fg$, $gh$ and $(fg)h$ are defined, but $f(gh)$ is not. A similar example may be constructed, where $f(gh)$ is defined but $(fg)h$ is not.

Example 2.5.

Let $\Lambda=\left\{f,g,h\right\}$ with product $fg=hh=h$. Then $(fg)h$ is defined, but $gh$ is not. A similar example may be constructed where $f(gh)$ is defined but $fg$ is not.

Example 2.6.

If $\Lambda$ is any set endowed with a non-associative binary operation, then (i)-(iii) of Definition 2.1 are always valid, and in particular equivalent, but $\Lambda$ is not a semigroupoid. For example, take $\Lambda=\left\{a,b\right\}$, $aa=ab=b$, $bb=ba=a$. Then $(aa)a=a$ but $a(aa)=b$.

Sub-semigroupoids and semigroupoid homomorphisms are defined in the natural manner.

Definition 2.7.

A sub-semigroupoid of a semigroupoid $\Lambda$ is a subset $\Delta\subseteq\Lambda$ such that $\Delta\Delta\subseteq\Delta$.

Definition 2.8.

A homomorphism between semigroupoids $\Lambda$ and $\Gamma$ is a map $\phi\colon\Lambda\to\Gamma$ such that $(\phi\times\phi)(\Lambda^{[2]})\subseteq\Gamma^{[2]}$ and $\phi(ab)=\phi(a)\phi(b)$ for all $(a,b)\in\Lambda^{[2]}$.

It is immediate to verify that if $\phi\colon \Lambda\to\Gamma$ is a homomorphism of semigroupoids and $\Delta$ is a sub-semigroupoid of $\Gamma$, then $\phi^{-1}(\Delta)$ is a sub-semigroupoid of $\Lambda$. However, contrary to the cases of semigroups and groupoids, the image of a homomorphism $\phi\colon\Lambda\to\Gamma$ between semigroupoids is not necessarily a sub-semigroupoid of $\Gamma$.

Example 2.9.

Let $\Lambda=\left\{e,f\right\}$, with operations $ee=e$ and $ff=f$ and $\Gamma=\left\{e,f,g\right\}$ the semigroup with product $ee=e$, $ff=f$, and all other products $xy=g$. Then the inclusion $\iota\colon\Lambda\hookrightarrow\Gamma$ is a semigroupoid homomorphism, but the image $\iota(\Lambda)=\left\{e,f\right\}$ is not sub-semigroupoid of $\Gamma$.

We will now consider semigroupoids in the sense of Tilson.

Definition 2.10 ([MR915990]).

A graphed semigroupoid is a tuple $(\mathcal{S}^{(0)},\mathcal{S},\so,\ra,\mu)$, where $(\mathcal{S}^{(0)},\mathcal{S},\so,\ra)$ is a graph and $\mu\colon\mathcal{S}^{(2)}\to\mathcal{S}$ is a product map, denoted by concatenation, $\mu(a,b)=ab$, satisfying:

  1. for all $(a,b)\in \mathcal{S}^{(2)}$, $\so(ab)=\so(b)$ and $\ra(ab)=\ra(a)$ ‒ i.e., $(\id_{\mathcal{S}^{(0)}},\mu)$ is a graph morphism;

  2. for all $(a,b,c)\in \mathcal{S}^{(3)}$, $(ab)c=a(bc)$.

We will always assume that a graphed semigroupoid $\mathcal{S}$ satisfies $\mathcal{S}^{(0)}=\so(\mathcal{S})\cup\ra(\mathcal{S})$. Otherwise, restricting the vertex set to $\so(\mathcal{S})\cup\ra(\mathcal{S})$ yields another graphed semigroupoid with the same underlying arrow set and product.

The next proposition shows that graphed semigroupoids are, in particular, Exel semigroupoids.

Proposition 2.11.

Let $(\mathcal{S}^{(0)},\mathcal{S},\so,\ra)$ be a graph and $\mu\colon\mathcal{S}^{(2)}\to \mathcal{S}$, $\mu(a,b)=ab$, a fixed function. Consider the following assertions:

  1. $(\mathcal{S}^{(0)},\mathcal{S},\so,\ra,\mu)$ is a graphed semigroupoid;

  2. $(\mathcal{S},\mathcal{S}^{(2)},\mu)$ is an Exel semigroupoid.

  3. for all $(a,b)\in \mathcal{S}^{(2)}$, $\so(ab)=\so(b)$ and $\ra(ab)=\ra(b)$.

Then (1) is equivalent to (2)+(3) (that is, their logical conjunction).

If $\mathcal{S}$ has no sources nor sinks, then (2) implies (3). (Thus (1) is equivalent to (2) in this case.)

Proof.

The implication (2)+(3)$\Rightarrow$(1) is trivial.

The only nontrivial part of the implication (1)$\Rightarrow$(2)+(3) is the verification that items (i)-(iii) of Definition 2.1 are equivalent: In other words, to compare when products $ab$, $bc$, $a(bc)$ and $(ab)c$ are defined.

For example, assume that 2.1(i) is valid, i.e., $(a,b)\in\mathcal{S }^{(2)}$ and $(b,c)\in\mathcal{S }^{(2)}$. Then $\so(ab)=\so(b)=\ra(c)$, so $(ab,c)\in\mathcal{S }^{(2)}$, which means that 2.1(ii) is valid. The other implications are proven similarly. Therefore (1) implies (2)+(3).

For the last part, assume that $(\mathcal{S },\mathcal{S }^{(2)},\mu)$ is an Exel semigroupoid and that the graph $\mathcal{S }$ has no sources nor sinks, and let us verify (3). Let $(a,b)\in\mathcal{S }^{(2)}$. As the vertex $\so(b)$ is not a source of $\mathcal{S }$, choose $z\in\mathcal{S }$ such that $(b,z)\in\mathcal{S }^{(2)}$. Then $(ab,z)\in\mathcal{S }^{(2)}$, because $(\mathcal{S },\mathcal{S }^{(2)},\mu)$ is an Exel semigroupoid, which means that $\so(ab)=\ra(z)=\so(b)$. Similarly, $\mathcal{S }$ not having sinks implies that $\ra(ab)=\ra(a)$. This is precisely property (3).

Example 2.12.

Every semigroup $S$ may be regarded as a graphed semigroupoid with a singleton vertex set, $S^{(0)}=\left\{\ast\right\}$. Conversely, every graphed semigroupoid (or rather its arrow set) with singleton vertex set is a semigroup.

We will now characterize Exel semigroupoids which admit a compatible graph structure (Proposition 2.15). These were already considered in [MR2419901]. We will moreover classify all compatible graph structures to such an Exel semigroupoid (Proposition 2.17).

Definition 2.13 ([MR2419901]).

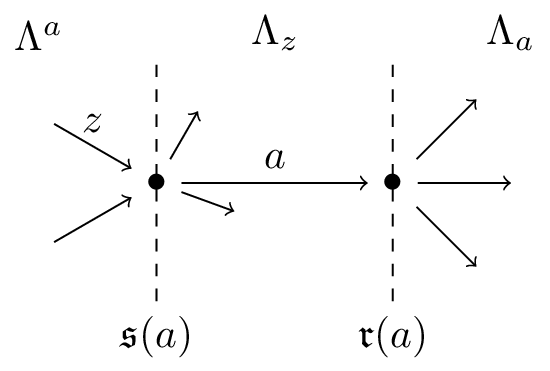
Let $\Lambda$ be an Exel semigroupoid. For every $a\in\Lambda$, we define

\begin{equation*} \Lambda^a=\left\{b\in\Lambda:(a,b)\in\Lambda^{[2]}\right\},\qquad\Lambda_a=\left\{b\in\Lambda:(b,a)\in\Lambda^{[2]}\right\}. \end{equation*}
We say that $\Lambda$ is categorical if for all $a,b\in\Lambda$, the sets $\Lambda^a$ and $\Lambda^b$ are either disjoint or equal.

Note that $b\in\Lambda^a$ if and only if $a\in\Lambda_b$. Moreover, $\Lambda^{ab}=\Lambda^b$ and $\Lambda_{ab}=\Lambda_a$ for all $(a,b)\in\Lambda^{[2]}$.

Proposition 2.14.

The following are equivalent for an Exel semigroupoid $\Lambda$:

  1. $\Lambda$ is categorical.

  2. For all $a,b\in\Lambda$, $\Lambda_a$ and $\Lambda_b$ are either disjoint or equal.

Proof.

Assume that $\Lambda$ is categorical and let $a,b\in\Lambda$. We need to prove that if $\Lambda_a$ and $\Lambda_b$ are not disjoint, then they are equal. Suppose $p\in\Lambda_a\cap\Lambda_b$. By symmetry, it is sufficient to prove that $\Lambda_a\subseteq\Lambda_b$.

Given $r\in\Lambda_a$, we have $a\in\Lambda^p\cap\Lambda^r$. Therefore, $\Lambda^p=\Lambda^r$, as $\Lambda$ is categorical. As $b\in\Lambda^p=\Lambda^r$, then $r\in\Lambda_b$. Therefore (2) is valid.

The implication (2)$\Rightarrow$(1) is completely analogous.

We will now prove that categorical semigroupoids are precisely those with a compatible graph structure. All that is needed is to define an appropriate vertex set and source and range maps. The main idea is that if $\mathcal{S}$ is a graphed semigroupoid and $(a,z)\in\mathcal{S }^{(2)}$, then for any other arrow $c\in\mathcal{S }$, we have $\so(c)=\so(a)$ if and only if $c\in\mathcal{S }_z$. This suggests us to identify $\so(a)$ with $\mathcal{S }_z$, and this is where the categorical property comes into play. If $\mathcal{S }^a=\varnothing$ (i.e., there is no $z$ such that $(a,z)\in\mathcal{S }^{(2)}$), then we add a “dummy” vertex as the source of $a$.

Theorem 2.15.

Every graphed semigroupoid is categorical. Conversely, every categorical Exel semigroupoid $(\Lambda,\Lambda^{[2]},\mu)$ can be graphed, i.e., we may construct a graphed semigroupoid $(\Lambda^{(0)},\Lambda,\so,\ra,\mu)$, in such a way that $\Lambda^{[2]}=\Lambda^{(2)}$.

Proof.

Suppose that $(\mathcal{S }^{(0)},\mathcal{S },\so,\ra,\mu)$ is a graphed semigroupoid and $a,b\in\mathcal{S }$. If $\mathcal{S }^a$ and $\mathcal{S }^b$ are not disjoint, take any $p\in\mathcal{S }^a\cap\mathcal{S }^b$. For all $q\in\mathcal{S }^a$, we have

\begin{equation*} \ra(q)=\so(a)=\ra(p)=\so(b) \end{equation*}
thus $q\in\mathcal{S}^b$. This proves $\mathcal{S }^a\subseteq\mathcal{S }^b$, and the reverse inclusion is proven similarly. Hence $\mathcal{S }$ is categorical.

Conversely, assume that $(\Lambda,\Lambda^{[2]},\mu)$ is a categorical semigroupoid. We will first construct the vertex set of the underlying graph of $\Lambda$.

Consider two collections of symbols

\begin{equation*} V_0=\left\{v_0(a):a\in\Lambda,\Lambda^a=\varnothing\right\}\qquad\text{and}\qquad V_1=\left\{v_1(a):a\in\Lambda,\Lambda_a=\varnothing\right\}. \end{equation*}
Let $R_0$ and $R_1$ be any two equivalence relations on $V_0$ and $V_1$, respectively, satisfying, for all $(a,b)\in\Lambda^{[2]}$,
\begin{equation*} \text{if }\Lambda^b=\varnothing\text{ then }(v_0(b),v_0(ab))\in R_0\qquad\text{and}\qquad\text{if }\Lambda_a=\varnothing\text{ then }(v_1(a),v_1(ab))\in R_1.\tag{2.16} \end{equation*}
We denote the $R_i$-equivalence class of a symbol $v_i(a)\in V_i$ as $[v_i(a)]$ (where $a\in\Lambda)$.

Define the vertex set $\Lambda_{R_0,R_1}^{(0)}$ as the disjoint union $\left\{\Lambda_a:a\in\Lambda,\Lambda_a\neq\varnothing\right\}\sqcup(V_0/R_0)\sqcup(V_1/R_1)$, and the source and range maps $\so_{R_0,R_1},\ra_{R_0,R_1}\colon\Lambda\to\Lambda_{R_0,R_1}^{(0)}$ as

\begin{equation*} \so_{R_0,R_1}(a)=\begin{cases} \Lambda_z,&\text{if }z\text{ is any element of } \Lambda^a\\ [v_0(a)],&\text{if }\Lambda^a=\varnothing, \end{cases}\qquad\text{and}\qquad \ra_{R_0,R_1}(a)=\begin{cases} \Lambda_a,&\text{if }\Lambda_a\neq\varnothing,\\ [v_1(a)],&\text{if }\Lambda_a=\varnothing. \end{cases} \end{equation*}
We need to check that the source map is well-defined: if $\Lambda^a$ is nonempty and $z_1,z_2\in\Lambda^a$, then $a\in\Lambda_{z_1}\cap\Lambda_{z_2}$, which is therefore nonempty and thus $\Lambda_{z_1}=\Lambda_{z_2}$ because $\Lambda$ is categorical. Moreover, note that if $z\in\Lambda^a$, then $a\in\Lambda_z\neq\varnothing$, so $\Lambda_z\in\Lambda_{R_0,R_1}^{(0)}$.

This defines a graph structure on $\Lambda$. Since it depends on $R_0$ and $R_1$, we denote the set of $2$-paths as $\Lambda_{R_0,R_1}^{(2)}$. We need to prove that $\Lambda^{[2]}=\Lambda_{R_0,R_1}^{(2)}$.

If $(a,b)\in\Lambda^{[2]}$, then $b\in\Lambda^a$, so $\so(a)=\Lambda_b$. Also, $a\in\Lambda_b$, which is nonempty and thus $\ra(b)=\Lambda_b=\so(a)$. This proves $\Lambda^{[2]}\subseteq\Lambda_{R_0,R_1}^{(2)}$.

Conversely, suppose that $(a,b)\in\Lambda_{R_0,R_1}^{(2)}$, that is, that $\so(a)=\ra(b)$. By the definitions of $\Lambda_{R_0,R_1}^{(2)}$ (as a disjoint union) and of the source and range maps, we necessarily have $\so(a)=\ra(b)\in\left\{\Lambda_z:z\in\Lambda\right\}$, that is, that $\so(a)=\Lambda_z$ for some $z\in\Lambda^a$, and that $\ra(b)=\Lambda_b$. Then

\begin{equation*} a\in\Lambda_z=\so(a)=\ra(b)=\Lambda_b, \end{equation*}
which means that $(a,b)\in\Lambda^{[2]}$.

Finally, since $\Lambda^{ab}=\Lambda^b$ and $\Lambda_{ab}=\Lambda_a$ for all $(a,b)\in\Lambda^{(2)}$, we obtain $\ra(ab)=\ra(a)$ and $\so(ab)=\so(b)$ (this is where Equation (2.16) is necessary). By Proposition 2.11, $(\Lambda_{R_0,R_1}^{(0)},\Lambda,\so,\ra,\mu)$ is a graphed semigroupoid.

The construction above, in fact, yields all the compatible graph structures on $\Lambda$, as we now prove. Let $V_0$ and $V_1$ be the two sets considered in the proof above.

Proposition 2.17.

Let $\Lambda$ be a categorical Exel semigroupoid, endowed with a graph structure which makes it a graphed semigroupoid $(\Lambda^{(0)},\Lambda,\so,\ra,\mu)$. Suppose, moreover, that $\Lambda^{(0)}=\so(\Lambda)\cup\ra(\Lambda)$.

Then there exist unique equivalence relations $R_0$ and $R_1$ on $V_0$ and $V_1$, respectively, and a bijection $I\colon\Lambda_{R_0,R_1}^{(0)}\to\Lambda^{(0)}$ such that $(I,\id_{\Lambda})$ is a graph isomorphism.

Proof.

Consider the sets

\begin{equation*} W_0=\left\{\so(a):\Lambda^a=\varnothing\right\},\qquad W_1=\left\{\ra(a):\Lambda_a=\varnothing\right\}\qquad\text{and}\qquad W=\Lambda^{(0)}\setminus(W_0\cup W_1). \end{equation*}
Note that $W_0$ and $W_1$ are disjoint, since otherwise there would be $a,b\in\Lambda$ such that $\so(a)=\ra(b)$ and $\Lambda_b=\varnothing$. However, this would imply that $(a,b)\in\Lambda^{(2)}$, so $a\in\Lambda_b$, a contradiction.

First we need to construct the equivalence relations $R_0$ and $R_1$ as in Proposition 2.15. Consider the functions $F_0\colon V_0\to W_0$ and $F_1\colon V_1\to W_1$ given by

\begin{equation*} F_0(v_0(a))=\so(a)\qquad\text{and}\qquad F_1(v_1(b))=\ra(b) \end{equation*}
for all $a,b\in\Lambda$ such that $\Lambda^a=\Lambda_b=\varnothing$. Note that these maps are surjective. Consider the equivalence relations $R_i=\ker F_i$ ($i=1,2$), that is,
\begin{equation*} R_i=\left\{(v_i(a),v_i(b)):F_i(v_i(a))=F_i(v_i(b))\right\}. \end{equation*}
Then Equation (2.16) is clearly satisfied, by the definition of $F_0$ and $F_1$ and because $\so$ and $\ra$ are compatible with the semigroupoid structure of $\Lambda$ (see Definition 2.10(ii)).

Therefore the maps $F_i$ factor through the quotient to bijections $V_i/R_i\to W_i$. This gives us a bijection

\begin{equation*} I\colon(V_0/R_0)\sqcup(V_1/R_1)\to W_0\cup W_1,\qquad I([v_i(a)])=F_i(v_i(a)). \end{equation*}
We need to extend $I$ to a bijection from $\Lambda_{R_0,R_1}^{(0)}$ to $\Lambda^{(0)}$, that is, we need to define $I(\Lambda_a)$ when $\Lambda_a\neq\varnothing$ in order to obtain a bijection from $\left\{\Lambda_a:\Lambda_a\neq\varnothing\right\}$ to $W$.

If $\Lambda_a\neq\varnothing$, we let $I(\Lambda_a)=\ra(a)$. In order to prove that $I$ is well-defined, suppose $\Lambda_{a_1}=\Lambda_{a_2}\neq\varnothing$. Choose any $z\in\Lambda_{a_1}=\Lambda_{a_2}$, so $(z,a_i)\in\Lambda^{(2)}$, that is, $\ra(a_1)=\so(z)=\ra(a_2)$, so $I(\Lambda_a)$ is uniquely defined.

Now let us prove that $I(\Lambda_a)\in W$ whenever $\Lambda_a\neq\varnothing$, or equivalently that $I(\Lambda_a)\not\in W_0\cup W_1$.

Therefore $I(\Lambda_a)\in\Lambda^{(0)}\setminus(W_0\cup W_1)=W$.

Let us now prove that every $v\in W$ is of the form $I(\Lambda_a)$ for some $a\in\Lambda$ with $\Lambda_a\neq\varnothing$. As we assume that $\Lambda^{(0)}=\so(\Lambda)\cup\ra(\Lambda)$, we have two possibilities:

We have thus obtained a surjection $I\colon\left\{\Lambda_a:\Lambda_a\neq\varnothing\right\}\to W$. We still need to prove that $I$ is injective on this set. Suppose $I(\Lambda_a)=I(\Lambda_b)$, that is, $\ra(a)=\ra(b)$, where $\Lambda_a,\Lambda_b\neq\varnothing$. Choose any $z\in\Lambda_a$. Then $\so(z)=\ra(a)=\ra(b)$, so $z\in\Lambda_a\cap\Lambda_b$, and therefore $\Lambda_a=\Lambda_b$ as $\Lambda$ is categorical.

We have, therefore, a well-defined bijection $I\colon\Lambda_{R_0,R_1}^{(0)}\to\Lambda^{(0)}$. We are done if we verify that $\so(a)=I(\so_{R_0,R_1}(a))$ and $\ra(a)=I(\ra_{R_0,R_1}(a))$ for all $a\in\Lambda$. Let $a\in\Lambda$. If $\Lambda^a=\varnothing$, then

\begin{equation*} I(\so_{R_0,R_1}(a))=I([v_0(a)])=F_0(v_0(a))=\so(a). \end{equation*}
If $\Lambda^a\neq\varnothing$, then we choose $z\in\Lambda^a$, so that $a\in\Lambda_z\neq\varnothing$, and
\begin{equation*} I(\so_{R_0,R_1}(a))=I(\Lambda_z)=\ra(z)=\so(a). \end{equation*}

This proves that $I\circ\so_{R_0,R_1}=\so$, and similarly $I\circ\ra_{R_0,R_1}=\ra$. Therefore $(I,\id_\Lambda)$ is a graph isomorphism.

Suppose now that $R_0'$ and $R_1'$ are any other equivalence relations on $V_0$ and $V_1$ and $J\colon\Lambda_{R_0',R_1'}^{(0)}\to\Lambda^{(0)}$ is any other bijection for which $(J,\id_{\Lambda})$ is a graph isomorphism. We denote the equivalence classes of $V_i/R_i'$ as $[v_i(a)]'$. For each $v_0(a),v_0(b)\in V_0$, where $\Lambda^a=\Lambda^b=\varnothing$, we have

\begin{equation*} \begin{array}{c c c c c} v_0(a)R_0'v_0(b)&\iff&[v_0(a)]'=[v_0(b)]'&\iff& J([v_0(a)]')=J([v_0(b)]')\\ &\iff& J(\so_{R_0',R_1'}(a))=J(\so_{R_0',R_1'}(b))&\iff& \so(a)=\so(b)\\ &\iff& F_0(v_0(a))=F_0(v_0(b))&\iff& v_0(a)R_0 v_0(b), \end{array} \end{equation*}
where we use the facts that $J$ is injective, the definition of the source map $\so_{R_0',R_1'}$, the fact that $(J,\id_{\Lambda})$ is a graph isomorphism, and the definitions of $F_0$ and of $R_0=\ker F_0$. Therefore $R_0'=R_0$. Similarly, $R_1'=R_1$.

Example 2.18.

Let $\Lambda=\left\{a,b,x,y,z\right\}$, with product defined by

\begin{equation*} aa=a,\quad xa=y,\quad ya=y,\quad bb=b, \quad xb=z,\quad zb=z \end{equation*}
Then $\Lambda$ is a non-categorical semigroupoid, since $\Lambda_a=\left\{x,y\right\}$ and $\Lambda_b=\left\{x,z\right\}$ are different but not disjoint. Thus $\Lambda$ cannot be fully realized as a graphed semigroupoid.

Note that every Exel semigroupoid $\Lambda$ may be identified, in an injective and homomorphic manner, as a subset of some semigroup $S$: Namely, the power set $S=2^\Lambda$ of $\Lambda$ is a semigroup under the product of sets, and the map $\phi\colon\Lambda\to S$, $\phi(a)=\left\{a\right\}$, is an injective semigroupoid homomorphisms. However, $\phi(\Lambda)$ is not a sub-semigroup(oid) of $S$ if $\Lambda$ is not a semigroup itself.

We finish this introduction by providing a condition that allows us to “extend” semigroupoid homomorphisms between graphed semigroupoids to graph homomorphisms.

Proposition 2.19.

Suppose that $G$ and $H$ are graphs, that $G$ has no sources nor sinks, and that $\phi\colon G\to H$ is a map such that $(\phi\times\phi)(G^{(2)})\subseteq H^{(2)}$. Then there exists a unique “vertex map” $\phi^{(0)}\colon G^{(0)}\to H^{(0)}$ such that $(\phi^{(0)},\phi)$ is a graph morphism.

Proof.

Uniqueness of such $\phi^{(0)}$ is immediate, since we require that $\so_H\circ\phi=\phi^{(0)}\circ\so_G$, and $\so_G$ is surjective as $G$ has no sinks. This same equation yields us the only possible formula for $\phi^{(0)}$, viz. $\phi^{(0)}(v)=\so_H(\phi(a))$ where $a\in G$ is any arrow with $\so_G(a)=v$. Thus we need to verify that $\so_G(a)=\so_G(b)$, where $a,b\in G$, implies $\so_H(\phi(a))=\so_H(\phi(b))$. As $\so_G(a)$ is not a source, there exists $z\in G$ with $\ra_G(z)=\so_G(a)=\so_G(b)$, that is $(a,z)$ and $(b,z)\in G^{(2)}$. Then $(\phi(a),\phi(z))$ and $(\phi(b),\phi(z))\in H^{(2)}$, which means that

\begin{equation*} \so_H(\phi(a))=\ra_H(\phi(z))=\so_H(\phi(b)). \end{equation*}
Therefore, we obtain a unique function $\phi^{(0)}\colon G^{(0)}\to H^{(0)}$ satisfying $\so_H\circ\phi=\phi^{(0)}\circ\so_G$. The proof that $\ra_H\circ\phi=\phi^{(0)}\circ\ra_G$ follows a similar argument as in the paragraph above, but using instead the fact that $G$ has no sinks.

Corollary 2.20.

Suppose that $\mathcal{S}$ and $\mathcal{T}$ are graphed semigroupoids, $\phi\colon\mathcal{S}\to\mathcal{T}$ is a semigroupoid homomorphism, and that $\mathcal{S}$ has no sources nor sinks. Then there exists a unique “vertex map” $\phi^{(0)}\colon\mathcal{S}^{(0)}\to\mathcal{T}$ such that $(\phi^{(0)},\phi)$ is a graph homomorphism.

Example 2.21.

The proposition above is not valid if we just assume that $\mathcal{S}$ has no sinks (or no sources). Let us associate a semigroupoid $A$ to the strict order of $\mathbb{N}$ in the same manner as we associate categories to (non-strict) orders ‒ namely $A=\left\{(n,m)\in\mathbb{N}\times\mathbb{N}:m\smallerthan n\right\}$, with product $(n,m)(m,k)=(n,k)$, vertex set $A^{(0)}=\mathbb{N}$ and source and range maps $\so(n,m)=m$, $\ra(n,m)=n$.

Now let $\mathcal{S}_1=A\sqcup A$ consist of two distinct copies of $A$, so $\mathcal{S}_1$ is a graphed semigroupoid over $\mathcal{S}_1^{(0)}=\mathbb{N}\sqcup\mathbb{N}$ (the product of $\mathcal{S}_1$ is defined only for elements in the same copy of $A$). We let $\mathcal{S}_2^{(0)}$ be the set obtained from $\mathcal{S}_1^{(0)}=\mathbb{N}\sqcup\mathbb{N}$ by identifying both copies of $0$, and let $\mathcal{S}_2$ be the graphed semigroupoid obtained from $\mathcal{S}_1$ by composing the source and range maps with the canonical quotient map $\mathcal{S}_1^{(0)}\to\mathcal{S}_2^{(0)}$.

Then neither $\mathcal{S}_1$ nor $\mathcal{S}_2$ have sinks, but the identity map $\mathcal{S}_2\to\mathcal{S}_1$ is an Exel semigroupoid isomorphism which cannot be extended to a graph homomorphism.

2.2. Inverse semigroupoids

The main goal of this subsection if to define inverse semigroupoids and to extend the basic elements of the theory of inverse semigroups to this more general setting.
Definition 2.22.

An Exel semigroupoid $\Lambda$ is regular if for every $a\in\Lambda$ there exists $b\in\Lambda$ such that $(a,b),(b,a)\in\Lambda^{[2]}$ and

\begin{equation*} aba=a\qquad\text{and}\qquad bab=b. \end{equation*}
Such an element $b$ is called an inverse of $a$.

If every element $a\in\Lambda$ admits a unique inverse, then $\Lambda$ is called an inverse semigroupoid. In this case, the unique inverse of $a$ is denoted $a^*$.

All groupoids and all inverse semigroups are inverse semigroupoids.

Just as in the case of semigroups, the condition for regular semigroupoids can be weakened to the following: For every $a\in\Lambda$, there exists $b\in\Lambda$ such that $aba=a$. Such an element $b$ is called a pseudoinverse of $a$. It follows that $bab$ is an inverse of $a$, and therefore $\Lambda$ is regular.

Example 2.23.

Suppose that $\Lambda$ is an inverse graphed semigroupoid, endowed with some compatible graph structure. Then for every $x\in\Lambda^{(0)}$, the isotropy semigroup $\Lambda_x^x=\ra^{-1}(x)\cap\so^{-1}(x)$ is in fact an inverse semigroup, with the product induced by $\Lambda$.

Given an Exel semigroupoid $\Lambda$, denote by $E(\Lambda)=\left\{e\in \Lambda:(e,e)\in\Lambda^{[2]}\text{ and }ee=e\right\}$ the set of idempotents of $\Lambda$. Note that if $t$ is an inverse of $s$, then $st$ and $ts$ are idempotents.

We will now proceed to prove that every inverse semigroupoid admits a unique compatible graph structure (Corollary 2.27).

Lemma 2.24.

Let $\Lambda$ be an inverse semigroupoid. The following are equivalent:

  1. $\Lambda$ is categorical;

  2. For all $e,f\in E(\Lambda)$, if $ef$ is defined, then $fe$ is also defined and $ef=fe$.

Proof. (1)$\Rightarrow$(2): Suppose that $\Lambda$ is categorical, and that $ef$ is defined, where $e,f\in E(\Lambda)$. We consider any compatible graph structure on $\Lambda$. Then $\so(f)=\ra(f)=\so(e)=\ra(e)$, so $fe$ is defined. Let $x=\so(e)$. Then $e$ and $f$ belong to the isotropy semigroup $\Lambda_x^x$ and are idempotents, therefore $ef=fe$ ([MR1455373]). (2)$\Rightarrow$(1): Assume (2) holds. We will construct an explicit compatible graph structure on $\Lambda$, although similar arguments may be used to prove directly that $\Lambda$ is categorical. We define the following equivalence relation $\sim$ on $E(\Lambda)$:
\begin{equation*} e\sim f\iff ef\text{ is defined}. \end{equation*}
The only nontrivial part about $\sim$ being an equivalence relation is transitivity. If $ef$ and $fg$ are defined ($e,f,g\in E(\Lambda)$), then $efg=(ef)(fg)=(fe)(gf)$, and in particular $eg$ is defined. Thus $\sim$ is transitive.

Denote the $\sim$-class of $e\in E(\Lambda)$ by $[e]$. Let $\Lambda^{(0)}=E(\Lambda)/\!\!\sim$, and define a graph structure on $\Lambda$ by setting

\begin{equation*} \so(a)=[a^*a],\qquad \ra(a)=[aa^*]. \end{equation*}
Since a product $ab$ is defined if and only if $a^*abb^*$ is defined, i.e., if and only if $\so(a)=\ra(b)$, we have $\Lambda^{[2]}=\Lambda^{(2)}$, as necessary. We may also compute, for all $(a,b)\in\Lambda^{(2)}$,
\begin{equation*} (ab)(ab)^*=(aa^*a)b(ab)^*=(aa^*)(ab)(ab)^*, \end{equation*}
so $\ra(ab)=\ra(a)$. Similarly, $\so(ab)=\so(b)$. By Proposition 2.11, $(\Lambda^{(0)},\Lambda,\so,\ra,\mu)$ is a graphed semigroupoid.

The set $\Lambda^{(0)}$ constructed above is the space of germs of $E(\Lambda)$ with its canonical order. This construction will be further developed in Subsection 4.3.

Theorem 2.25.

Every inverse semigroupoid $\Lambda$ is categorical. Equivalently, if $e,f\in E(\Lambda)$ and $ef$ is defined, then $fe$ is also defined and $ef=fe$.

Proof.

We will prove that $\Lambda$ satisfies condition (2) of Lemma 2.24, which follows the same arguments as in the case of inverse semigroups (see [MR1455373]), as long as we make sure that all products involved are defined. We include the details for completeness. Suppose that $e,f\in E(\Lambda)$, and that $(e,f)\in \Lambda^{[2]}$. Let $x=(ef)^*$. Then

\begin{equation*} (ef)x(ef)=ef\qquad\text{and}\qquad x(ef)x=x \end{equation*}
In particular, the products $fx$ and $xe$ are defined, so $fxe$ is defined. Let us prove that $fxe=x$, by proving that $fxe$ is an inverse of $ef$: Since $ff=f$ and $ee=e$ are defined, then we may compute
\begin{equation*} (fxe)(ef)(fxe)=fx(e^2)(f^2)xe=fxefxe=fxe\tag{2.26} \end{equation*}
and similarly $(ef)(fxe)(ef)=ef$. Thus $fxe$ is the inverse of $ef$, i.e., $fxe=x$. Moreover, it follows from the last equality of (2.26) that
\begin{equation*} x=fxe=fxefxe=x^2 \end{equation*}
so $x\in E(\Lambda)$, and in particular $x=x^*=ef$ is idempotent.

Since $fx=f(ef)$ is defined, then $fe$ is defined, and the same argument as above (changing the roles of $e$ and $f$) proves that $fe\in E(\Lambda)$. To finish, we use the equalities $x=fxe=ef$ to obtain

\begin{equation*} fe=fefe=fxe=x=ef. \end{equation*}

Therefore, every inverse semigroupoid admits a compatible graph structure. Suppose $\mathcal{S}$ is a graphed inverse semigroupoid. Recall that we assume that $\mathcal{S}^{(0)}=\so(\mathcal{S})\cup\ra(\mathcal{S})$. Given $a\in \mathcal{S}$, $a^*a$ and $aa^*$ are defined, so $\so(a)=\ra(a^*)$ and $\ra(a)=\so(a^*)$. It follows that $\mathcal{S}$ has no sources nor sinks. From Corollary 2.20 we may conclude that the compatible graph structure is unique.

Corollary 2.27.

If $\Lambda$ is an inverse semigroupoid, then there exists a unique compatible graph structure on $\Lambda$.

We will thus always regard inverse semigroupoids as graphed semigroupoids, with their unique compatible graph structure, and for every inverse semigroupoid homomorphism $\phi\colon\mathcal{S}\to\mathcal{T}$, we denote $\phi^{(0)}\colon\mathcal{S}^{(0)}\to\mathcal{T}^{(0)}$ the unique map for which $(\phi^{(0)},\phi)$ is a graph homomorphism, as in Corollary 2.20.

Let $\mathcal{S}$ be an inverse semigroupoid. We will now list the remaining algebraic properties of $\mathcal{S}$ which will be used in the remainder of this article.

Definition 2.28.

The canonical order of an inverse semigroup $\mathcal{S}$ is the relation $\leq$ defined as

\begin{equation*} a\leq b\iff a=ba^*a. \end{equation*}
(In particular, we require that $\so(a)=\so(b)$ and $\ra(a)=\ra(b)$.)

Note that inverse semigroupoid homomorphisms preserve the order.

If a product $ab$ is defined in the inverse semigroupoid $\mathcal{S}$, then $\ra(a^*)=\so(a)=\ra(b)=\so(b^*)$, so $b^*a^*$ is also defined. Using this and the commutativity of $E(\mathcal{S})$, the properties below can be proven by the same computations as in the case of inverse semigroups. See [MR1455373] for details.

Proposition 2.29.

Let $\mathcal{S}$ be an inverse semigroupoid. Then

  1. $(ab)^*=b^*a^*$, for all $(a,b)\in\mathcal{S}^{(2)}$.

  2. If $e\in E(\mathcal{S})$ and $(b,e)\in \mathcal{S}^{(2)}$. then $beb^*\in E(\mathcal{S})$.

  3. the following are equivalent:

    1. $a\leq b$;

    2. there exists $e\in E(\mathcal{S})$ such that $a=be$;

    3. there exists $f\in E(\mathcal{S})$ such that $a=fb$;

    4. $a^*\leq b^*$.

  4. $\leq$ is a partial order on $\mathcal{S}$;

  5. If $a\leq b$, $c\leq d$ and $(a,c)\in \mathcal{S}^{(2)}$, then $ac\leq bd$.

We may determine subclasses of the class of semigroupoids algebraically as follows: An inverse semigroupoid $\mathcal{S}$ is a

2.3. A representation theorem

Cayley's theorem states that every group can be represented as a permutation group on some set. More generally, the Vagner-Preston theorem states that every inverse semigroup can be represented as a semigroup of partial bijections on some set. In this subsection, we will further generalize this to represent semigroupoids as certain semigroupoids of partial bijections.

Representation results have been obtained in the context of inverse categories, i.e., (possibly large) categories which behave as inverse semigroupoids. Namely, it is proven that every (locally small) inverse category may be faithfully embedded into the category $\cat{PInj}$ of sets and partial bijections. For more details, see [MR0506554], [MR1871071], [MR3093088]. However we adopt a fundamentally different perspective from those works, by considering inverse semigroupoids as innate to bundles. This approach has the advantage of making the dynamical nature of inverse semigroupoids more explicit, and in particular to naturally motivating a natural notion of action for inverse semigroupoids.

Let $\pi\colon X\to X^{(0)}$ be a bundle. A partial bijection between fibers of $\pi$ is a triple $(y,f,x)$, where $x,y\in X^{(0)}$ and $f\colon\dom(f)\to\ran(f)$ is a bijection with $\dom(f)\subseteq\pi^{-1}(x)$ and $\ran(f)\subseteq\pi^{-1}(y)$ (in other words, $f$ is a partial bijection from $\pi^{-1}(x)$ to $\pi^{-1}(y)$). We denote by $\mathcal{I}(\pi)$ the set of all partial bijections between fibers of $\pi$.

We make $\mathcal{I}(\pi)$ into a graph over $X^{(0)}$ by setting

\begin{equation*} \so(y,f,x)=x\qquad\text{and}\qquad\ra(y,f,x)=y \end{equation*}
and then induce a product structure on $\mathcal{I}(\pi)$ as
\begin{equation*} (z,g,y)(y,f,x)=(z,g\circ f,x) \end{equation*}
where $g\circ f$ is the usual partial composition of functions
\begin{equation*} g\circ f\colon f^{-1}(\ran(f)\cap\dom(g))\to g(\dom(g)\cap\ran(f)),\qquad (g\circ f)(x)=g(f(x)). \end{equation*}

The verification that this products makes $\mathcal{I}(\pi)$ into an inverse semigroupoid is straightforward. The inverse of an element $(y,f,x)$ is $(x,f^{-1},y)$, where $f^{-1}\colon\ran(f)\to\dom(f)$ is the inverse function of $f$. The idempotent set of $\mathcal{I}(\pi)$ is

\begin{equation*} E(\mathcal{I}(\pi))=\left\{(x,\id_A,x):x\in X^{(0)},A\subseteq\pi^{-1}(x)\right\}. \end{equation*}

In particular cases, this construction leads to well-known examples of semigroups and groupoids.

Example 2.30.

Suppose that $X$ is a set, seen as a bundle over a singleton set $X^{(0)}=\left\{\ast\right\}$, i.e., we consider the bundle $\pi\colon X\to\left\{\ast\right\}$, $\pi_X(x)=\ast$ for all $x\in X$. Then $\mathcal{I}(X)\defeq\mathcal{I}(\pi)$ is simply the inverse semigroup of partial bijections of $X$.

Example 2.31.

Consider the identity function $\id_X$ of a set $X$. Let $L_2=\left\{0,1\right\}$ be the lattice with two elements $0\smallerthan 1$, which is an inverse semigroup under meets. Let $X\times X$ be the transitive equivalence relation on $X$, seen as a groupoid. Then $\mathcal{I}(\id_X)$ is isomorphic to the product inverse semigroupoid $(X\times X)\times L_2$ (where the product semigroupoid structure is defined in the obvious manner). Namely, to an element $(y,f,x)$ of $\mathcal{I}(\id_X)$ we associate the element $(y,x,0)$ of $(X\times X)\times L_2$ if $f=\varnothing$, the empty function, and $(y,x,1)$ otherwise.

Note that the equivalence relation $X\times X$ is isomorphic to the subsemigroupoid of maximal elements (with respect to the canonical order) of $(X\times X)\times L_2$, or to the initial groupoid of $\mathcal{I}(\id_X)$ (see Subsection 4.3).

We now state our representation theorem for inverse semigroupoids.

Theorem 2.32.

Let $\mathcal{S}$ be an inverse semigroupoid. Then $\mathcal{S}$ is isomorphic to a sub-inverse semigroupoid of $\mathcal{I}(\pi)$ for some bundle $\pi$.

Proof.

Considering the range map $\ra\colon\mathcal{S}\to \mathcal{S}^{(0)}$, we will define an embedding $\alpha\colon\mathcal{S}\to\mathcal{I}(\ra)$. Namely, given $a\in\mathcal{S}$, $\alpha(a)$ is a triple of the form $(y,\alpha_a,x)$, where $x,y\in\mathcal{S}^{(0)}$ and $\alpha_a$ is a partial bijection from $\ra^{-1}(x)$ to $\ra^{-1}(y)$. We first describe the map $\alpha_a$.

For every $a\in\mathcal{S}$, let $D_a=\left\{t\in \mathcal{S}:tt^*\leq aa^*\right\}$. If $t\in D_{a^*}$, then

\begin{equation*} (at)(at)^*=att^*a^*\leq aa^*, \end{equation*}
so $at\in D_a$. Therefore we may define $\alpha_a\colon D_{a^*}\to D_a$ as $\alpha_a(t)=at$. It is a bijection, since if $t\in D_{a^*}$, then $\alpha_a(t)\in D_a$, so we may apply $\alpha_{a^*}$ and obtain
\begin{equation*} \alpha_{a^*}(\alpha_a(t))=\alpha_{a^*}(at)=a^*at=t, \end{equation*}
because $tt^*\leq a^*a$. This proves that $\alpha_{a^*}\circ\alpha_a=\id_{D_{a^*}}$. Changing the roles of $a^*$ and $a$ we conclude that $\alpha_a$ is invertible, with $\alpha_a^{-1}=\alpha_a^*$.

Moreover, we have $D_a\subseteq\ra^{-1}(\ra(a))$ and thus we may define $\alpha\colon \mathcal{S}\to\mathcal{I}(\ra)$ by

\begin{equation*} \alpha(a)=(\ra(a),\alpha_a,\so(a)). \end{equation*}
Notice that, for $a,b\in\mathcal{S}$,
\begin{equation*} ab\text{ is defined}\iff\so(a)=\ra(b)\iff\so(\alpha(a))=\ra(\alpha(b))\iff\alpha(a)\alpha(b)\text{ is defined}.\tag{2.33} \end{equation*}
Using the equivalence above and the same arguments as in the proof of the Vagner-Preston theorem (see [MR1724106], for example), it follows that $\alpha$ is an injective semigroupoid homomorphism. In fact, the right-to-left implications of 2.33 imply that the image of $\alpha$ is a sub-semigroupoid of $\mathcal{I}(\ra)$, onto which $\alpha$ is an isomorphism.

Still considering the map $\alpha$ of the proof above, note that the vertex set of $\mathcal{I}(\ra)$ is $\mathcal{S}^{(0)}$, the vertex set of $\mathcal{S}$. We have $\so\circ\alpha=\so$, so the “vertex map” (as in Corollary 2.20) associated to $\alpha$ is the identity of $\mathcal{S}^{(0)}$. This motivates the definition of an action of an inverse semigroupoid $\mathcal{S}$ on a set $X$.

Definition 2.34.

A global action of an inverse semigroupoid $\mathcal{S}$ on a set $X$ consists of a map $\pi\colon X\to\mathcal{S}^{(0)}$, called the anchor map and a semigroupoid homomorphism $\theta\colon\mathcal{S}\to\mathcal{I}(\pi)$ such that the vertex map $\theta^{(0)} \colon\mathcal{S}^{(0)}\to\mathcal{I}(\pi)^{(0)}=\mathcal{S}^{(0)}$ is the identity $\id_{\mathcal{S}^{(0)}}$.

More explicitly, it consists of a map $\pi\colon X\to\mathcal{S}^{(0)}$ and a family $\left\{\theta_a:a\in\mathcal{S}\right\}$ of bijections $\theta_a\colon\dom(\theta_a)\to\ran(\theta_a)$ such that

  1. $\dom(\theta_a)\subseteq\pi^{-1}(\so(a))$ and $\ran(\theta_a)\subseteq\pi^{-1}(\ra(a))$ for all $a\in\mathcal{S}$;

  2. $\theta_{a}\circ\theta_b=\theta_{ab}$ for all $(a,b)\in\mathcal{S}^{(2)}$.

However, as stated in the introduction, we will be interested in more general notions than actions, which is the content of the next subsection.

2.4. $\land$-prehomomorphisms, partial homomorphisms, and actions

Generalizations of homomorphisms, initially called $\lor$ and $\land$-prehomomorphisms, were respectively introduced in [MR0424979] and [MR0470123] by McAlister and Reilly on their study of $E$-unitary inverse semigroups. We will focus on $\land$-prehomomorphisms, which are appropriate for the constructions of semidirect products.

Remark

The terminology “prehomomorphism” has been used to describe $\lor$-prehomomorphisms in [MR1694900], but used to describe $\land$-prehomomorphisms in [MR752899] and [Mikola2017]. In order to avoid confusion, we will use the original terminology of “$\land$-prehomomorphism”.

A more specific case of $\land$-prehomomorphisms are partial homomorphisms, whose study was initiated by Exel in [MR1276163], in order to describe the structure of C*-algebras endowed with an action of the circle. This turned out to be a rich area of research, with several applications in the theory of topological dynamical systems and C*-algebras (see [MR2799098], MR3699795]). Let us mention that partial homomorphisms of general inverse semigroups were first defined in [MR3231479], while partial actions of groupoids (on rings) were defined in [MR2982887].

We will now define $\land$-prehomomorphisms and partial homomorphisms in the context of semigroupoids, connecting in a precise manner all the notions described above. From them, we will construct semidirect products in a manner which generalizes semidirect products of groupoids ([MR2273730]), transformation groupoids of partial group actions ([MR2045419]), semidirect products of inverse semigroups acting on semilattices (see [MR0357660.1] and [MR752899]). Similarly, groupoids of germs of (partial) inverse semigroup actions are simply the underlying groupoids of the associated semidirect product (see Section 4).

Definition 2.35.

Let $\mathcal{S}$ and $\mathcal{T}$ be inverse semigroupoids and $\theta\colon\mathcal{S}\to\mathcal{T}$ a function. Consider the following statements:

  1. For all $a\in\mathcal{S}$ we have $\theta(a^*)=\theta(a)^*$;

  2. For all $a,b\in\mathcal{S}^{(2)}$, we have $(\theta(a),\theta(b))\in\mathcal{T}^{(2)}$ and $\theta(a)\theta(b)\leq\theta(ab)$;

  3. If $a\leq b$ in $\mathcal{S}$, then $\theta(a)\leq\theta(b)$ in $\mathcal{T}$.

If $\theta$ satisfies (i)-(ii), then $\theta$ is called a $\land$-prehomomorphism. If $\theta$ satisfies all of (i)-(iii), then $\theta$ is called a partial homomorphism.

Example 2.36.

Let $\mathcal{S}$ be any inverse semigroupoid, $X$ any set, and consider $2^X$, the power set of $X$, as a semigroup under intersection.

If $X$ has sufficiently large cardinality (e.g. $|X|\geq|\mathcal{S}|$), then there is a map $\theta\colon\mathcal{S}\to 2^X\setminus\left\{\varnothing\right\}$ such that $\theta(a)\cap\theta(b)=\varnothing$ if $a\neq b$. Then $\theta$ is a $\land$-prehomomorphism, but not a partial homomorphism as long as $\mathcal{S}$ is not a groupoid.

If $\theta\colon\mathcal{S}\to\mathcal{T}$ is a $\land$-prehomomorphism, then $\theta$ takes idempotents to idempotents. Indeed, if $e\in E(\mathcal{S})$, then $\theta(e)^*\theta(e)=\theta(e^*)\theta(e)\leq\theta(e^*e)=\theta(e)$. Applying the definition of the order of $\mathcal{T}$ implies $\theta(e)=\theta(e)^*\theta(e)$, which is idempotent.

Following [MR1694900], two elements $a,b\in\mathcal{S}$ are compatible if $a^*b$ and $ab^*$ are idempotent. Any $\land$-prehomomorphism $\theta\colon\mathcal{S}\to\mathcal{T}$ takes compatible elements to compatible elements, if $a,b\in\mathcal{S}$ are compatible, then $\theta(a)^*\theta(b)\leq\theta(a^*b)$, which is idempotent. Similarly, $\theta(a)\theta(b)^*$ is idempotent.

The statements 2.35.(i)-(iii) are independent, that is, there exist maps $\theta\colon\mathcal{S}\to\mathcal{T}$ between inverse semigroupoids which satisfy any two of them but not the third one. In fact, we can obtain such examples for inverse semigroups, which we present for the sake of reference.

Example 2.37.

Let $G=\left\{1,g\right\}$ be the cyclic group of order $2$ and $X=\left\{a,b\right\}$. Define $\theta\colon G\to\mathcal{I}(X)$ as $\theta_1=\id_X$ and

\begin{equation*} \theta_g\colon\left\{a\right\}\to\left\{b\right\},\qquad\theta_g(a)=b. \end{equation*}
Then $\theta$ satisfies 2.35(ii) and (iii), but not (i).

Example 2.38.

Let $G=\left\{1\right\}$ be the trivial group, and $H=\left\{1,g\right\}$ the cyclic group of order $2$. The map $\theta\colon G\to H$, $1\mapsto g$ satisfies 2.35(i) and (iii), but not (ii).

Example 2.39.

Let $L_2=\left\{0,1\right\}$ be the lattice with two elements, $0\smallerthan 1$, and define $\theta\colon L_2\to L_2$ as $\theta(a)=b$ and $\theta(b)=\theta(a)$. Then 2.35(i) and (ii) are satisfied, but (iii) is not (i.e., $\theta$ is a $\land$-prehomomorphisms but not a partial homomorphism).

We should remark that $\land$-prehomomorphisms are not stable under composition.

Example 2.40.

Let $S=\left\{a,b\right\}$ and $\theta$ be as in Example 2.39. Let $G=\left\{1,g\right\}$ be the group with two elements and $\eta\colon G\to S$ be given by $\eta(1)=b$, $\eta(g)=a$. Then $\theta$ is a $\land$-prehomomorphism and $\eta$ is a partial homomorphism, however $\theta\circ\eta$ is not a $\land$-prehomomorphism since

\begin{equation*} \theta(\eta(g))\theta(\eta(g))=\theta(a)\theta(a)=bb=b\qquad\text{and}\qquad\theta(\eta(gg))=\theta(\eta(1))=\theta(b)=a. \end{equation*}

On the other hand, it is easy to verify that if $\eta$ is a $\land$-prehomomorphism and $\theta$ is a partial homomorphism, then $\theta\circ\eta$ is a $\land$-prehomomorphism, and also that the composition of two partial homomorphisms is a partial homomorphism.

We may now define $\land$-preactions and partial actions. In particular from property 2.35(ii), we may apply Proposition 2.19 to obtain a unique map $\phi^{(0)}\colon\mathcal{S}^{(0)}\to\mathcal{T}^{(0)}$ such that $(\phi^{(0)},\phi)$ is a graph homomorphism.

Definition 2.41.

A $\land$-preaction of an inverse semigroupoid $\mathcal{S}$ on a set $X$ consists of an anchor map $\pi\colon X\to\mathcal{S}^{(0)}$ and a $\land$-prehomomorphism $\theta\colon \mathcal{S}\to\mathcal{I}(\pi)$ such that the vertex map $\theta^{(0)}$ is the identity of $\mathcal{S}^{(0)}$. If $\theta$ is a partial homomorphism, we call $(\pi,\theta)$ a partial action. We say that $(\pi,\theta)$ is non-degenerate if $X=\bigcup_{a\in\mathcal{S}}\dom(\theta_a)$.

We use the notation $(\pi,\theta)\colon\mathcal{S}\curvearrowright X$ to denote a $\land$-preaction of $\mathcal{S}$ on $X$.

As $\land$-prehomomorphisms take idempotents to idempotents, then whenever $(\pi,\theta)\colon\mathcal{S}\curvearrowright X$ is a $\land$-preaction and $e\in E(\mathcal{S})$, the map $\theta_e$ is the identity of its domain. Moreover, if $a\in\mathcal{S}$, then

\begin{equation*} \theta_a=\theta_a\theta_a^{-1}\theta_a\leq\theta_a\theta_{a^*a} \end{equation*}
which implies that $\dom(\theta_a)\subseteq\dom(\theta_{a^*a})$.

If $a\leq b$ and $x\in\dom(a^*a)\cap\dom(b)$, then we may compute

\begin{equation*} \theta_b(x)=\theta_b(\theta_{a^*a}(x))=\theta_{ba^*a}(x)=\theta_a(x).\tag{2.42} \end{equation*}
Note, however, that we do not necessarily have $\dom(\theta_a)\subseteq\dom(\theta_b)$ (unless $(\pi,\theta)$ is a partial action), so we need some care with these computations.

These notions extend, simultaneously, those of (global) actions and partial actions which have commonly appeared throughout the literature.

Example 2.43.

Let $S$ be an inverse semigroup, so $S^{(0)}=\left\{\ast\right\}$ is a singleton. Given any set $X$, there is a unique map $\pi\colon X\to S^{(0)}$. Therefore, partial and global actions of $S$ on $X$, as an inverse semigroupoid, are the same as partial and global actions of $S$ on $X$ in the usual sense of inverse semigroups (see e.g. [MR2565546] and [MR3231479]).

Example 2.44.

If $\mathcal{G}$ is a groupoid, then a non-degenerate global action $(\pi,\theta)\colon\mathcal{G}\curvearrowright X$ is the same as a groupoid action as in [MR2969047] or [MR2273730], i.e., it satisfies $\dom(\theta_a)=\pi^{-1}(a)$ for all $a\in\mathcal{S}$.

Indeed, as $\theta$ is a global action then $\dom(\theta_a)=\dom(\theta_{a^*a})=\dom(\theta_{\so(a)})$ for all $a\in\mathcal{S}$. That is, $\dom(\theta_a)$ depends only on $\so(a)$, so if $\so(a)=\so(b)$ then $\dom(\theta_a)=\dom(\theta_b)$. Non-degeneracy of $(\pi,\theta)$ means precisely that for all $a\in A$, $\pi^{-1}(\so(a))=\bigcup_{b\in\so^{-1}(\so(a))}\dom(\theta_b)=\dom(\theta_a)$, as we wanted.

In order to construct semidirect products, we will need to consider $\land$-preactions which preserve the structure of semigroupoids. This notion will be used to connect the topological and algebraic settings (i.e., when considering appropriate actions of semigroupoids on topological spaces and on algebras).

Definition 2.45.

A left ideal of a semigroupoid $\Lambda$ is a subset $I\subseteq\Lambda$ such that $\Lambda I\subseteq I$. Right ideals are defined similarly. An ideal is a subset of $\Lambda$ which is simultaneously a left and a right ideal.

Example 2.46.

Let $\mathcal{G}$ be a groupoid. The map $I\mapsto\so(I)$ is an order isomorphism from the set of ideals of $\mathcal{G}$ to the set of invariant subsets of $\mathcal{G}^{(0)}$ (a subset $A\subseteq\mathcal{G}^{(0)}$ is invariant if $A=\ra(\so^{-1}(A))$).

Every set $X$ is regarded as a groupoid in the trivial manner: $X^{(0)}=X$, and for all $x\in X$, $\so(x)=\ra(x)=x$, and the product is defined as $xx=x$. The groupoids constructed in this manner are called unit groupoids. Ideals of $X$ are precisely its subsets.

If $\Lambda$ is an Exel semigroupoid, a homomorphism $\phi\colon\Lambda\to X$ is a function such that, if $(a,b)\in\Lambda^{[2]}$, then $\phi(a)=\phi(b)$. In particular, functions between sets are the same as their (semi)groupoid homomorphisms.

In the definition below, we regard the vertex set $\mathcal{S}^{(0)}$ as a unit groupoid. This is an adaptation of [MR2982887]

Definition 2.47.

A $\land$-preaction (resp. partial, global action) $(\pi,\theta$) of an inverse semigroupoid $\mathcal{S}$ on a semigroupoid $\Lambda$ is a $\land$-preaction (resp. partial, global action) of $\mathcal{S}$ on $\Lambda$, as a set, which further satisfies:

  1. The anchor map $\pi\colon\Lambda\to\mathcal{S}^{(0)}$ is a homomorphism.

  2. For every $x\in\mathcal{S}^{(0)}$, $\pi^{-1}(x)$ is an ideal of $\Lambda$;

  3. For every $a\in\Lambda$, $\dom(\theta_a)$ is an ideal of $\pi^{-1}(\so(a))$;

  4. For every $a\in\mathcal{S}$, $\theta_a$ is a semigroupoid isomorphism from $\dom(\theta_a)$ to $\ran(\theta_a)$.

Remark

  1. Alternatively to (ii) and (iii), we could adopt the simpler (and slightly stronger) assumption that $\dom(\theta_a)$ is an ideal of $\Lambda$ for all $a\in\mathcal{S}$. This is the case, for example, when all such ideals $\dom(\theta_a)$ are idempotent (see Definition 2.60).

  2. If $\Lambda$ is a set/unit groupoid, then this definition coincides with 2.41, since the additional properties of Definition 2.47 become trivial. Accordingly, by a $\land$-preaction we will always mean one in the sense of Definition 2.47.

As we will be more interested in continuous $\land$-preactions of topological semigroupoids, we refer to Subsection 3.1 for examples. In fact, every $\land$-preaction $(\pi,\theta)\colon\mathcal{S}\curvearrowright\Lambda$ may be “extended” to a partial action, in the sense that partial action $(\pi,\overline{\theta})\colon\mathcal{S}\curvearrowright\Lambda$ (with same anchor map) such that $\theta_a\leq\overline{\theta}_a$ for all $a\in\mathcal{S}$. See Proposition 2.48

Let us finish this subsection by proving that any $\land$-preaction may be “extended” to a partial action.

Proposition 2.48.

Let $(\pi,\theta)\colon\mathcal{S}\curvearrowright\Lambda$ be a $\land$-preaction. Then there exists a partial action $(\pi,\overline{\theta})\colon\mathcal{S}\curvearrowright\Lambda$ such that $\theta_a\leq\overline{\theta}_a$ for all $a\in\mathcal{S}$.

Proof.

As the only (possible) problem with is that $\theta$ does not necessarily satisfy $\theta_b\leq\theta_a$ when $b\leq a$, we simply “glue” $\theta_b$ to $\theta_a$ in this case.

More precisely: Let $a\in\mathcal{S}$. If $b_1,b_2\leq a$. Then $b_1$ and $b_2$ are compatible, so $\theta_{b_1}$ and $\theta_{b_2}$ are compatible (see the paragraphs after Definition 2.35), which means that $\theta_{b_1}$ and $\theta_{b_2}$ coincide on the intersection of their domains, as do $\theta_{b_1}^{-1}$ and $\theta_{b_2}^{-1}$.

Thus we set $\overline{\theta}_a=\bigvee_{b\leq a}\theta_b$, the join taken in $\mathcal{I}(\Lambda)$ i.e., $\overline{\theta}_a(x)$ is defined if and only if $\theta_b(x)$ is defined for some $b\leq a$, in which case $\overline{\theta}_a(x)=\theta_b(x)$. This defines an isomorphism between the ideals $\bigcup_{b\leq a}\dom(\theta_b)$ of $\pi^{-1}(\so(a))$ and $\bigcup_{b\leq a}\ran(\theta_b)$ of $\pi^{-1}(\ra(a))$. It is clear that $\overline{\theta}_{a^*}=\overline{\theta}_a^{-1}$, and that $\overline{\theta}$ is order preserving, and the verification that it is a $\land$-preaction, and thus a partial action, is straightforward.

Note that the partial action $(\pi,\overline{\theta})$ constructed above is minimal, in the sense that any other partial action $(\pi,\gamma)$ extending $(\pi,\theta)$ satisfies $\overline{\theta}_a\leq\gamma_a$ for all $a\in\mathcal{S}$.

2.5. Semidirect products

Throughout this subsection, we fix a $\land$-preaction $(\pi,\theta)\colon\mathcal{S}\curvearrowright \Lambda$. Consider the set

\begin{equation*} \mathcal{S}\ltimes\Lambda=\left\{(a,x)\in\mathcal{S}\times X:x\in\dom(\theta_a)\right\}. \end{equation*}
We will endow $\mathcal{S}\ltimes\Lambda$ with a product, and call the resulting semigroupoid the semidirect product of $(\pi,\theta)$. If $(a,x)$ and $(b,y)\in\mathcal{S}\ltimes\Lambda$, $ab$ and $x\theta_b(y)$ are defined (in $\mathcal{S}$ and $\Lambda$, respectively), we set
\begin{equation*} (a,x)(b,y)=(ab,\theta_{b^*}(x\theta_b(y))).\tag{2.49} \end{equation*}
(Compare this formula with the product on partial crossed product algebras; see [arxiv1804.00396], MR1456588], MR1331978].)

To check that the right-hand side of (2.49) is a well-defined element of $\mathcal{S}\ltimes\Lambda$, first note that $\theta_b(y)$ belongs to the ideal $\dom(\theta_{b^*})$ of $\Lambda$, so $\theta_{b^*}(x\theta_b(y))$ is an element of $\dom(\theta_b)$. We have

\begin{equation*} \theta_b(\theta_{b^*}(x\theta_b(y)))=x\theta_b(y). \end{equation*}
Since $x$ belongs to the ideal $\dom(\theta_a)$, then $\theta_{b^*}(x\theta_b(y))$ belongs to $\dom(\theta_a\circ\theta_b)$, which is contained in $\dom(\theta_{ab})$ because $\theta$ is a $\land$-prehomomorphism. Therefore $(ab,\theta_{b^*}(x\theta_b(y)))\in\mathcal{S}\ltimes\Lambda$.

However, the product (2.49) is not associative in general, even when considering global actions of inverse semigroups on semigroups. The example below is a slight modification of [MR2115083].

Example 2.50.

Let $G=\left\{1,g\right\}$ be the cyclic group of order $2$, and $S$ the inverse semigroup obtained by adjoining a new unit $x$ to $G$.

Let $T=\left\{0,t,u,v\right\}$ be the semigroup with product defined by

\begin{equation*} tv=vt=u\qquad\text{and}\qquad ab=0\quad\text{if}\quad(a,b)\not\in\left\{(t,v),(v,t)\right\}. \end{equation*}
Consider the ideal $I=\left\{0,u,v\right\}$ of $T$, and define an action $\theta\colon S\curvearrowright T$ as $\theta_x=\id_T$, $\quad\theta_1=\id_I$ and $\theta_g\colon I\to I$ as
\begin{equation*} \theta_g(0)=0,\qquad\theta_g(u)=v\qquad\text{and}\qquad\theta_g(v)=u. \end{equation*}

Then $(1,t)((g,u)(1,t))=(g,0)$, but $((1,t)(g,u))(1,t)=(g,u)$.

Definition 2.51.

We call $\mathcal{S}\ltimes\Lambda$ with the product (2.49) the semidirect product semigroupoid (induced by the $\land$-preaction $(\pi,\theta)$), whenever the product (2.49) is associative.

We will therefore need to consider conditions on the $\land$-preaction $\theta\colon\mathcal{S}\curvearrowright\Lambda$ which make the product in (2.49) associative, so that we obtain a semigroupoid structure on $\mathcal{S}\ltimes\Lambda$. The same ideas as in [MR2115083], which lie in the context of partial actions of groups on algebras, may be easily adapted to the context of semigroupoid actions and show that the product (2.49) is in fact associative for a large class of inverse semigroupoid actions. See the paragraph after Proposition 2.61

Definition 2.52.

A multiplier of a semigroupoid $\Lambda$ is a pair $(L,R)$, of partially defined maps $L$ and $R$ on $\Lambda$ satisfying

  1. $\dom(L)$ is a right ideal of $\Lambda$ and $\dom(R)$ is a left ideal of $\Lambda$;

  2. $L(ab)=L(a)b$;

  3. $R(ab)=aR(b)$;

  4. $R(a)b=aL(b)$,

in the sense that each side of these equations is defined if and only if the other side is defined, in which case they coincide. $L$ and $R$ are called, respectively, a left and a right multipliers.

Example 2.53.

Given $x\in\Lambda$, we let $L_x\colon\Lambda^x\to x\Lambda^x$ and $R_x\colon \Lambda_x\to\Lambda_xx$ be given by $L_x(a)=xa$ and $R_x(a)=ax$. Then $(L_x,R_x)$ is a multiplier. If $I$ is an ideal of $\Lambda$, then the restrictions of $L_x$ and $R_x$ to $I$ form a multiplier of $I$.

Definition 2.54.

$\Lambda$ is non-degenerate if the map $a\mapsto (L_a,R_a)$ is injective.

Moreover, the associative property of $\Lambda$ may be rewritten in terms of multipliers as follows: For all $a,b\in\Lambda$,

\begin{equation*} \dom(L_a)\cap\dom(R_b)\subseteq\dom(L_a\circ R_b)\qquad\text{and}\qquad L_a\circ R_b=R_b\circ L_a. \end{equation*}

Definition 2.55.

A semigroupoid $\Lambda$ is $(L,R)$-associative if for any two multipliers $(L,R)$ and $(L',R')$ of $\Lambda$, we have

\begin{equation*} \dom(L)\cap\dom(R')\subseteq\dom(L\circ R')\qquad\text{and}\qquad L\circ R'=R'\circ L \end{equation*}

Theorem 2.56.

The product of $\mathcal{S}\ltimes\Lambda$ is associative if $\dom(\theta_a)$ is $(L,R)$-associative for all $a\in\mathcal{S}$.

Proof.

Let $(a,r),(b,s),(c,t)\in \mathcal{S}\ltimes\Lambda$. As long as it makes sense, we compute

\begin{equation*} \left((a,r)(b,s)\right)(c,t)=\left(ab,\theta_{b}^{-1}(r\theta_{b}(s))\right)(c,t)=(abc,\theta_{c}^{-1}(\theta_{b}^{-1}(r\theta_{b}(s))\theta_{c}(t))) \end{equation*}
and
\begin{equation*} (a,r)\left((b,s),(c,t)\right)=(a,r)\left(bc,\theta_{c}^{-1}(s\theta_{c}(t))\right)=(abc,\theta_{bc}^{-1}(r\theta_{bc}(\theta_{c}^{-1}(s\theta_{c}(t))))) \end{equation*}
Thus, we need to prove that for all $(a,b,c)\in\mathcal{S}^{(3)}$,
\begin{equation*} \theta_{c}^{-1}(\theta_{b}^{-1}(r\theta_{b}(s))\theta_{c}(t))=\theta_{bc}^{-1}(r\theta_{bc}(\theta_{c}^{-1}(s\theta_{c}(t)))) \end{equation*}
in the sense that either side is defined if and only if the other one is, and in which case the equation holds. As $\theta_c(t)$ runs through all of $\ran(\theta_c)$, let us rewrite it as $\theta_c(t)=w$. Let us first rewrite the right-hand side. We have
\begin{equation*} \theta_{bc}(\theta_c^{-1}(sw)=\theta_{bcc^*}(sw) \end{equation*}
and the element $sw$ belongs to the domains of both $\theta_{bcc^*}$ and of $\theta_b$. As $bcc^*\leq b$ then $\theta_{bcc^*}(sw)=\theta_b(sw)$ (see Equation (2.42)), thus we need instead to prove
\begin{equation*} \theta_{c}^{-1}(\theta_{b}^{-1}(r\theta_{b}(s))w)=\theta_{bc}^{-1}(r\theta_b(sw))\tag{2.57}. \end{equation*}

To further simplify the expression above we would need to rewrite the term “$\theta_{bc}^{-1}$”, at the beggining of the right-hand side above, as “$\theta_c^{-1}\circ\theta_b^{-1}$”, however this is not so immediate. If this is the case, Equation (2.57) implies

\begin{equation*} \theta_{b}^{-1}(r\theta_{b}(s))w=\theta_{b}^{-1}(r\theta_{b}(sw)).\tag{2.58} \end{equation*}

Let us postpone the proof of the equivalence (2.57)$\iff$(2.58) and instead finish the proof of the theorem. Then (2.58) may be rewritten as

\begin{equation*} R_{w}\circ \theta_{b}^{-1}\circ L_{r}\circ\theta_{b}=\theta_{b}^{-1}\circ L_{r}\circ \theta_{b}\circ R_{w}\tag{2.59} \end{equation*}
on $\dom(\theta_{b})$. Here we regard $L_r$ as a left multiplier of $\ran(\theta_b)$, as in Example 2.53, thus $\theta_{b}^{-1}\circ L_{r}\circ\theta_{b}$ is a left multiplier of $\dom(\theta_{b})$. Similarly, we regard $R_w$ as a right multiplier of $\dom(\theta_{b})$. As we assume that $\dom(\theta_{b})$ is $(L,R)$-associative, then Equation (2.59) holds.

In particular, this also proves that $((a,r)(b,s))(c,t)$ is defined if and only if $(a,r)((b,s)(c,t))$ is defined, which is equivalence (ii)$\iff$(iii) of Definition 2.1. We still need to prove that these terms are defined when both $(a,r)(b,s)$ and $(b,s)(c,t)$ are defined..

Indeed, in this case, $\theta_b^{-1}(r\theta_b(s))$ and $s\theta_c(t)$ are defined, which means that

\begin{equation*} s\in\dom(\theta_b^{-1}\circ L_r\circ\theta_b)\cap\dom(R_{\theta_c(t)})\subseteq\dom(R_{\theta_c(t)}\circ(\theta_b^{-1}\circ L_r\circ\theta_{b^{-1}})) \end{equation*}
because $\theta_b^{-1}\circ L_r\circ\theta_b$ and $R_{\theta_c(t)}$ are left and a right multipliers on $\dom(\theta_b)$, respectively. Then
\begin{equation*} \theta_b^{-1}(r\theta_b(s))\theta_c(t) \end{equation*}
is defined, thus $((a,r)(b,s))(c,t)$ is also defined.

Proof of the equivalence of Equations (2.57) and (2.58).

First assume that (2.57) holds. We may apply $\theta_c$ on the left-hand side, and hence on the right-hand side as well, to obtain

\begin{equation*} \theta_b^{-1}(r\theta_b(s))w=\theta_c(\theta_{(bc)^*}(r\theta_b(sw)))=\theta_{cc^*b^*}(r\theta_b(sw))=\theta_b^{-1}(r\theta_b(sw)), \end{equation*}
where the last equality follows from the fact that $cc^*b^*\leq b^*$ and $r\theta_b(sw)$ belongs to $\dom(\theta_{cc^*b^*})\cap\dom(\theta_b^*)$. This is precisely (2.58).

In the other direction, note that the left-hand side of (2.58) is $\theta_b^{-1}(r\theta_b(s))w$, and $w\in\ran(\theta_c)=\dom(\theta_{c^*})$. Thus we may apply $\theta_c^{-1}$ on both sides and use $\theta_c^{-1}\circ\theta_b^{-1}\leq\theta_{bc}^{-1}$ to obtain (2.57).

Proposition 2.61 below yields a large class of $(L,R)$-associative semigroupoids.

Definition 2.60.

$\Lambda$ is idempotent if $\Lambda=\Lambda\Lambda$, that is, if every $a\in\Lambda$ may be rewritten as a product $a=a_1a_2$, where $a_1,a_2\in\Lambda$.

Proposition 2.61.

A semigroupoid $\Lambda$ is $(L,R)$-associative if any of the following two conditions below holds.

  1. $\Lambda$ is idempotent;

  2. $\Lambda$ is non-degenerate, and for every $a\in\Lambda$ we have $\Lambda_a\neq\varnothing$.

  3. $\Lambda$ is non-degenerate, and for every $a\in\Lambda$ we have $\Lambda^a\neq\varnothing$.

Proof.

Let $(L,R)$ and $(L',R')$ be multipliers of $\Lambda$.

First assume that $a=a_1a_2$ in $\Lambda$. Then

\begin{equation*} L(R'(a))=L(R'(a_1a_2))=L(a_1R'(a_2))=L(a_1)R'(a_2)=R'(L(a_1)a_2)=R'(L(a_1a_2))=R'(L(a)). \end{equation*}
Thus if $\Lambda$ is idempotent, then $L\circ R'=R'\circ L$ as well.

Alternatively, for all $a,b$ we have

\begin{equation*} L(R'(a))b=L(R'(a)b)=L(aL'(b))=L(a)L'(b)=R'(L(a))b, \end{equation*}
and
\begin{equation*} bL(R'(a))=R(b)R'(a)=R'(R(b)a)=R'(bL(a))=bR'(L(a)), \end{equation*}
in the sense that, in each of these chains of equalities, one of the terms is defined if and only if the other ones are, in which case they coincide. If $\Lambda$ is non-degenerate, this implies that $L(R'(a))=R'(L(a))$ for all $a\in\Lambda$, i.e., $L\circ R'=R'\circ L$.

It remains only to prove that, under either of the hypotheses (i) or (ii) above, we have $\dom(L)\cap\dom(R')\subseteq\dom(L\circ R')$. Fix $a\in\dom(L)\cap\dom(R')$.

First assume that $\Lambda$ is idempotent, and write $a=a_1a_2$. Then we may compute

\begin{equation*} L(a)=L(a_1a_2)=L(a_1)a_2\qquad\text{and}\qquad R'(a)=R'(a_1a_2)=a_1R'(a_2). \end{equation*}
In particular, $a_1\in\dom(L)$, which is a right ideal and thus $a_1R'(a_2)\in\dom(L)$, so we may compute
\begin{equation*} L(a_1R'(a_2))=L(R'(a_1a_2))=L(R'(a)), \end{equation*}
and so $a\in\dom(L\circ R')$.

Now assume that condition (ii) holds, and take $x\in\Lambda_{L(a)}$, so $xL(a)=R(x)a$ is defined. Since $a$ belongs to the left ideal $\dom(R')$, we may compute

\begin{equation*} R'(R(x)a)=R(x)R'(a)=xL(R'(a)), \end{equation*}
and in particular $a\in\dom(L\circ R')$. The proof that condition (iii) implies $(L,R)$-associativity is similar.

We could also adapt the terminology “$s$-unital” from ring theory (see [MR0419511]) to the setting of semigroupoids: A semigroupoid $\Lambda$ is left $s$-unital if for every $t\in\Lambda$ there exists $u\in\Lambda_t$ such that $ut=t$. Of course every left $s$-unital semigroupoid is idempotent (and also non-degenerate). Examples of left $s$-unital semigroupoids include regular semigroupoids and categories ‒ in particular sets, groupoids, regular semigroups, multiplicative semigroups of $s$-unital rings, monoids, lattices etc…

Note that if $\Lambda$ is a regular semigroupoid, $I$ is an ideal of $\Lambda$, $x\in I$ and $y$ is an inverse of $x$ in $\Lambda$, then $y=yxy\in I$. It follows that $I$ itself is a regular semigroupoid. In particular, a $\land$-preaction $(\pi,\theta)\colon\mathcal{S}\curvearrowright\Lambda$ of an inverse semigroupoid $\mathcal{S}$ on a regular semigroupoid $\Lambda$ will always have the product (2.49) associative. In this case, $\mathcal{S}\ltimes\Lambda$ is also a regular semigroupoid, and in fact the converse implication is also true.

Proposition 2.62.

Suppose that the $\land$-preaction $(\pi,\theta)$ is non-degenerate and $\mathcal{S}\ltimes\Lambda$ is a semigroupoid. Then $\mathcal{S}\ltimes\Lambda$ is regular (resp. inverse) if and only if $\Lambda$ is regular (resp. inverse).

Proof.

We may simply prove that the inverses of $(a,x)\in\mathcal{S}\ltimes X$ are precisely the elements of the form $(a^*,\theta_a(x))$, where $y$ is an inverse of $x$ in $\Lambda$.

First assume that $(a,x)\in\mathcal{S}\ltimes\Lambda$, and that $x$ has an inverse $y$. Then as $y=yxy$ is defined, so $y\in p^{-1}(\so(a))$, and as $\dom(\theta_a)$ is an ideal of $p^{-1}(\so(a))$ then $y\in\dom(\theta_a)$. It is easy to verify that $(a^*,\theta_a(y))$ is an inverse of $(a,x)$.

Conversely, suppose that $(a,x)$ has an inverse $(b,z)$ in $\mathcal{S}\ltimes\Lambda$. This means that

\begin{equation*} (a,x)=(aba,\theta_{a^*}(\theta_{b^*}(x\theta_b(z))\theta_a(x)))\qquad\text{and}\qquad (z,y)=(zaz,\theta_{b^*}(\theta_{a^*}(z\theta_a(x))\theta_b(z))), \end{equation*}
so $b=a^*$. In particular $\theta_b=\theta_a^{-1}$, so using the fact that $\theta_a$ is a semigroupoid homomorphism, the equations above mean that
\begin{equation*} (a,x)=(a,x\theta_{a^*}(z)x)\qquad\text{and}\qquad (a^*,z)=(a^*,z\theta_a(x)z).\tag{2.63} \end{equation*}
The second equation above implies that
\begin{equation*} \theta_{a^*}(z)=\theta_{a^*}(z\theta_a(x)z)=\theta_{a^*}(z)x\theta_{a^*}(z). \end{equation*}
Together with the first equation of (2.63), this means that the element $y=\theta_{a^*}(z)$ is an inverse of $x$ in $\Lambda$, and $z=\theta_a(y)$.

The graphed case

If $\mathcal{T}$ is a graphed semigroupoid and $(\pi,\theta)\colon\mathcal{S}\curvearrowright\mathcal{T}$ is a $\land$-preaction, the semidirect product $\mathcal{S}\ltimes\mathcal{T}$ has a natural graphed structure over $\mathcal{T}^{(0)}$ (or more precisely, its subset $\bigcup_{a\in\mathcal{S}}\dom(\theta_a)$. Namely, the source and range maps of $\mathcal{S}\ltimes\mathcal{T}$ are defined as

\begin{equation*} \so(a,x)=\so(x)\qquad\text{ and }\ra(a,x)=\ra(\theta_a(x)). \end{equation*}